Hallo patlican68,
Zeichne vom Mittelpunkt \(M_1\) des kleinen Kreises eine Verbindung zum Punkt \(B\) des Quadrats.
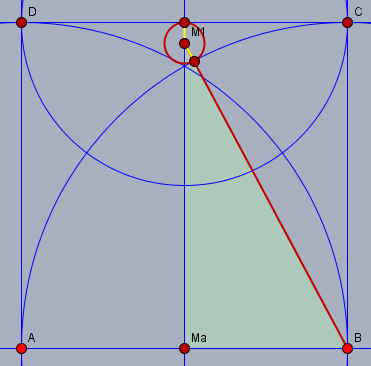
Der Mittelpunkt der unteren Quadratseite \(a=AB\) sei \(M_a\). Dann ist \(\triangle M_aBM_1\) ein rechtwinkliges Dreieck. Der Radius des kleinen Kreises sei \(r_1\) (gelb) und die Quadratseite habe die Länge \(a\) (rot). Nach Pythagoras ist dann $$\begin{aligned}\left(\frac a2\right) ^2 + (a-r_1)^2 &= (a+r_1)^2 \\\frac 14 a^2 + a^2 - 2ar_1 + r_1^2 &= a^2 +2ar_1 +r_1^2 \\ \frac14 a^2 &= 4ar_1 \\ r_1 &= \frac 1{16 }a\end{aligned}$$
Zeichne nun vom Mittelpunkt \(M_2\) des größeren Kreises (grün) ebenso eine Verbindung nach \(B\).
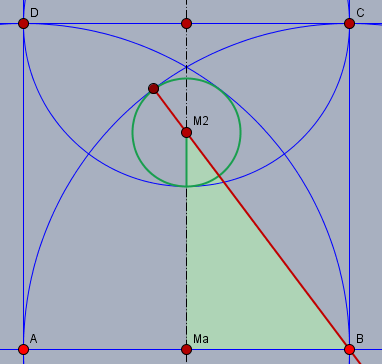
Der Radius dieses Kreises sei \(r_2\) (grün). Wieder ist das Dreieck \(\triangle M_aBM_2\) ein rechtwinkliges. Pythagoras anwenden: $$\begin{aligned} \left( \frac a2\right)^2 + \left( \frac a2 + r_2 \right)^2 &= (a-r_2)^2 \\ \frac14 a^2 + \frac14 a^2 + ar_2 + r_2^2 &= a^2 - 2ar_2 + r_2^2 \\ 3 ar_2 &= \frac 12 a^2 \\ r_2 &= \frac 16 a \end{aligned}$$ Gruß Werner