Ich glaube nicht, dass Ihr schon die exakte PQRSTUVW-Formel hattet, denn da kommen extrem lange Formeln heraus:
x1=(sqrt((2 (9 + sqrt(768081)))^(1/3) - 80 (3/(9 + sqrt(768081)))^(1/3)) - sqrt(80 (3/(9 + sqrt(768081)))^(1/3) - (2 (9 + sqrt(768081)))^(1/3) + 12/sqrt((2 (9 + sqrt(768081)))^(1/3) - 80 (3/(9 + sqrt(768081)))^(1/3))))/(2 6^(1/3))
=-1.69747188084416...
mit sqrt(x)=x^(1/2)=Wurzel(x)
Die anderen 3 unterscheiden sich nur durch Vorzeichen.
http://www.lamprechts.de/gerd/php/gleichung-6-grades.php
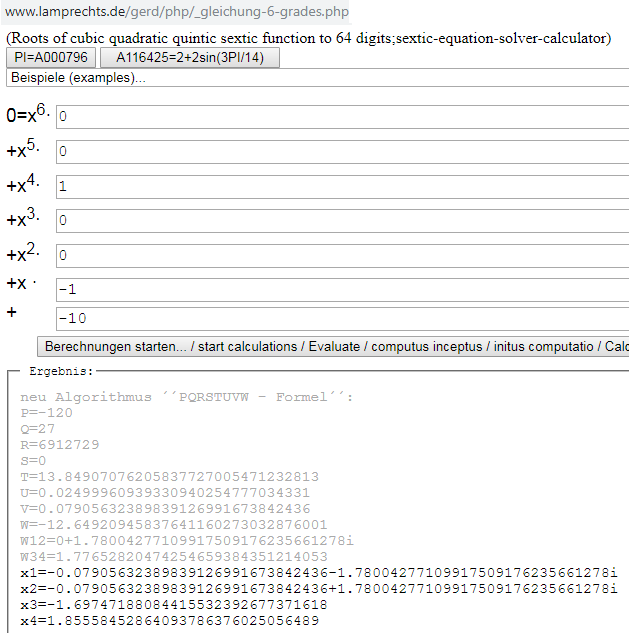
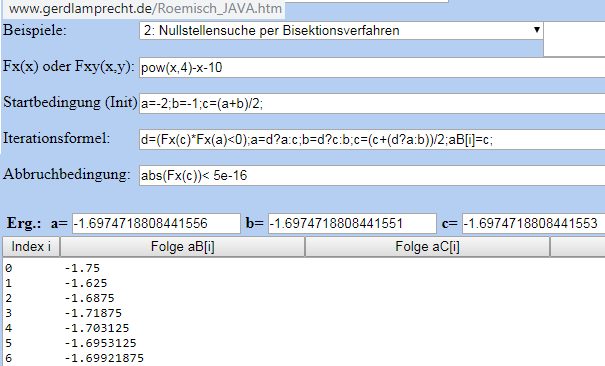
Was immer schon seit Beginn der Grundrechenarten funktioniert ist die https://de.wikipedia.org/wiki/Bisektion
Der Iterationsrechner unter
http://www.gerdlamprecht.de/Roemisch_JAVA.htm rechnet das im Beispiel 2 vor:
Lehrer geben jedoch meist Spezialfall-Aufgaben auf, wo sich was herauskürzt oder Substitution oder Raten ein einfaches Ergebnis ergibt.
Falsch abgeschrieben oder ausgedacht?