zunächst solltest Du Dich vergewissern, dass alle vier Punkte in einer Ebene liegen. Dies ist hier einfach, da alle vier Punkte die identische Y-Koordinate \(y=1\) haben. Folglich lässt sich das Viereck auch leicht in der Ebene \(y=1\) zeichnen:
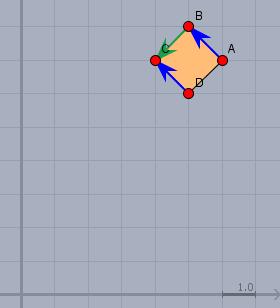
Nach rechts geht die X-Achse und nach oben die Z-Achse. Klick auf das Bild, dann öffnet sich eine 3D-Ansicht, die Du mit der Maus bewegen kannst.
Es gibt viele Möglichkeiten, zu prüfen, ob es sich bei dem Viereck um um ein Quadrat handelt. Eine einfache besteht darin, zunächst die Vektoren zweier gegenüberliegender Kanten zu berechnen. Z.B.: $$\vec{AB} = B-A = \begin{pmatrix} 5\\ 1\\ 8\end{pmatrix} - \begin{pmatrix}6 \\ 1\\7 \end{pmatrix} = \begin{pmatrix} -1\\ 0\\ 1\end{pmatrix} \\ \vec{DC} = C -D = \begin{pmatrix} 4\\ 1\\ 7\end{pmatrix} - \begin{pmatrix} 5\\1 \\ 6 \end{pmatrix} = \begin{pmatrix} -1\\ 0\\ 1\end{pmatrix}$$ Die Vektoren habe ich oben blau eingezeichnet. Du kannst in der Zeichnung das Ergebnis überprüfen. Man kommt vom Punkt \(A\) nach \(B\) indem man einen Schritt in negative Richtung \(x=-1\) also nach links macht und einen Schritt in positive Richtung \(z=1\) also nach oben macht. Der Vektor muss also \(\vec{AB} = \begin{pmatrix} x=-1 & y=0 & z=1\end{pmatrix}^T\) heißen. \(y\) bleibt \(0\) , da sich der Y-Wert zwischen den Punkten nicht ändert.
Du siehst, dass die Vektoren identisch sind. Damit ist bereits gezeigt, dass das Viereck alle Eigenschaften eines Parallelogramms hat. Nun berechne den Vektor einer dritten Seite - z.B.:$$\vec{BC} = C - B = \begin{pmatrix} 4 \\ 1 \\ 7\end{pmatrix} - \begin{pmatrix} 5\\ 1\\ 8\end{pmatrix} = \begin{pmatrix} -1\\ 0\\ -1\end{pmatrix}$$ diesen Vektor habe ich grün eingezeichnet. Wenn dieser Vektor so lang ist wie \(\vec{AB}\), so liegt eine Raute vor (alle vier Seiten sind dann gleich lang): $$|\vec{AB}| = \sqrt{(-1)^2 + 0^2 + 1^2} = \sqrt{2} \\ |\vec{BC}| = \sqrt{(-1)^2 + 0^2 + (-1)^2} = \sqrt{2}$$das ist erfüllt. Als letztes prüfe noch, ob zwei benachbarte Vektoren senkrecht zueinander stehen. Das macht man mit Hilfe des Skalarprodukts, was dann =0 werden muss.$$\vec{AB} \cdot \vec{BC} = \begin{pmatrix} -1\\ 0\\ 1\end{pmatrix} \cdot \begin{pmatrix} -1\\ 0\\ -1\end{pmatrix} = (-1)\cdot(-1) + 0 + 1\cdot(-1) = 1 - 1 = 0$$also handelt es sich um ein Quadrat.
Gruß Werner