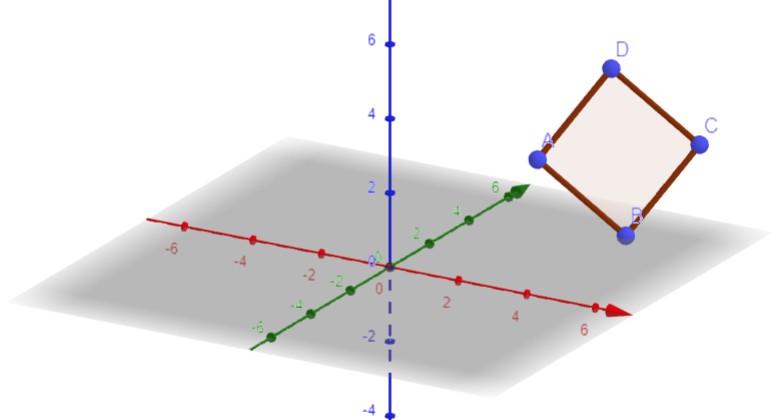
A(2,4,2), B(4,5,0), C(5,7,2), D(3,6,4)
Abstand von A nach B
|AB| = √((4 - 2)^2 + (5 - 4)^2 + (0 - 2)^2) = 3
Ebenso andere Abstände
|AD| = √((3 - 2)^2 + (6 - 4)^2 + (4 - 2)^2) = 3
|BC| = √((5 - 4)^2 + (7 - 5)^2 + (2 - 0)^2) = 3
|CD| = √((3 - 5)^2 + (6 - 7)^2 + (4 - 2)^2) = 3
Damit sind alle 3 Seiten gleich lang und das Viereck wäre eine Raute/Rombus.
|BD| = √((3 - 4)^2 + (6 - 5)^2 + (4 - 0)^2) = 3·√2
Nun gilt der Satz des Pythagoras
|AB|^2 + |AD|^2 = |BD|^2
3^2 + 3^2 = (3·√2)^2
Damit ist bei A ein rechter Winkel. Und dazu musste es sich, wenn es sich um ein ebenes Viereck handelt ein Quadrat sein.
Bei Bedarf könnte man aber auch noch die Rechtwinkligkeit an den Punkten B, C und D prüfen.
So schaut das in Geogebra aus