Ich habe das Bild übernommen und ein wenig ergänzt: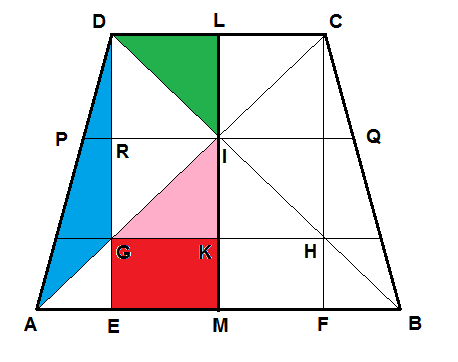
Wegen der Achsensymmetrie betrachte ich auch nur die linke Hälfte des Trapezes.
Die pinkfarbene und die grüne Fläche haben den gleichen Flächeninhalt. Begründung. Das Viereck CDGH ist ein Rechteck, welches durch die Symmetrieachse LM und die Gerade PQ in vier kongruente, also deckungs- und damit auch flächengleiche Rechtecke geteilt wird. Insbesondere sind die Rechtecke RILD und GKIR deckungsgleich. Da diese beiden Rechtecke durch die Diagonalen AC bzw. BD halbiert werden, müssen auch ihre Hälften und insbesondere also die Dreiecke DLI (grün) und GKI (pink) den gleichen Flächeninhalt haben.
Es verbleibt noch zu zeigen, dass das Rechteck EMKG (rot) und das Dreieck AGD (blau) den gleichen Flächeninhalt haben.
Bezeichnet man die Grundseite des Trapezes mit a und die gegenüberliegende Seite mit c, dann gilt:
EM = c / 2
AE = ( a - c ) / 2
Bezeichnet man weiterhin die Strecke ED mit h (Höhe des Trapezes) und die Strecke EG mit h1, dann gilt für den Flächeninhalt A der roten Fläche:
A = h1 * c / 2
Da die Dreiecke AED und AEG rechtwinklig sind, gilt für den Flächeninhalt B der blauen Fläche:
B = F ( AED ) - F ( AEG ) = ( ED * AE / 2 ) - ( EG * AE / 2 ) = ( ED - EG ) * AE / 2
= ( ( h - h1 ) * ( a - c ) / 2 ) / 2
= ( h - h1 ) * ( a - c ) / 4
Die Flächeninhalte A und B sind also gleich, wenn gilt:
A = B
<=> h1 * c / 2 = ( h - h1 ) * ( a - c ) / 4
<=> 2 * h1 * c = ( h - h1 ) * ( a - c ) = ha - hc - h1a + h1c
<=> h1c = ha - hc - h1a
<=> h1c + h1a = ha - hc
<=> h1 ( ( a + c ) = h ( a - c )
<=> h1 / h = ( a - c ) / ( a + c )
[Und genau diese Beziehung zwischen h1 und h besteht in dem Trapez und zwar aufgrund des Strahlensatzes.
Nach diesem gilt nämlich:
AE / EG = AF / FC
wobei AF = ( a / 2 ) + ( c / 2 ) = ( a + c ) / 2 ist]:
<=> ( ( a - c ) / 2 ) / h1 = ( ( a + c ) / 2 ) / h
<=> h1 / h = ( ( a - c ) / 2 ) / ( ( a + c ) / 2 ) = ( a - c ) / ( a + c )
Also haben die Flächen A (rot) und B (blau) den gleichen Flächeninhalt.