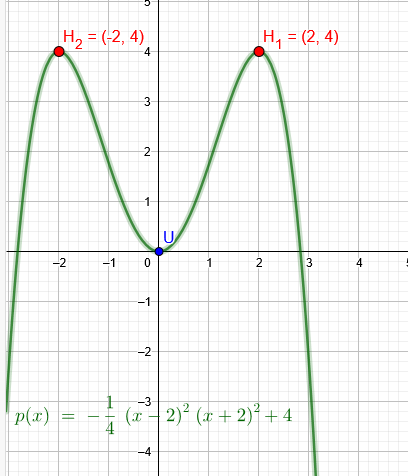
Der Graph einer zur Ordinatenachse achsensymmetrischen ganzrationalen Funktion 4. Grades verläuft durch den Ursprung und hat einen Hochpunkt H\( (2|\red{4})\)
Ich verschiebe den Graph um \(\red{4}\) Einheiten nach unten: \(H_1´(2|0)\)
Da der Graph achsensymmetrisch ist, gilt \(H_2´(-2|0)\)
Da nun auf der x-Achse Extremwerte sind, habe ich 2 doppelte Nullstellen.
Somit weiter mit der Nullstellenform der Funktion 4. Grades:
\(f(x)=a(x-2)^2(x+2)^2\)
...verläuft durch den Ursprung U\((0|0)\) → U´\((0|-4)\):
\(f(0)=a(0-2)^2(0+2)^2=16a=-4\)
\(a=-\frac{1}{4}\)
\(f(x)=-\frac{1}{4}(x-2)^2(x+2)^2\)
Nun um 4 Einheiten nach oben schieben:
\(p(x)=-\frac{1}{4}(x-2)^2(x+2)^2+4\)