Untersuchen Sie, wo die Temperaturabnahme maximal ist (Sinus Kurve soll Temperaturänderung beschreiben)

Question

Aufgabe:

Die Funktion lautet:$$f(x) = 3\cdot \sin \left( \frac {\pi}{12} (x - 11,5) \right) +33$$

Zeichnung: (y-Achse = Temperatur; x-Achse Zeit in Stunden)

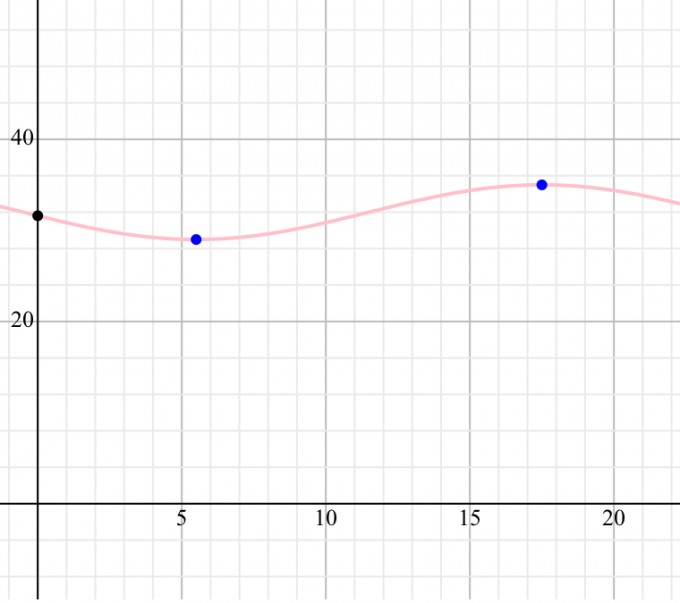
Die Frage ist: Untersuchen Sie,

bei welcher Temperatur ist die Temperaturabnahme maximal ist

Problem/Ansatz:

Soweit ich weiß handelt es sich hier

um einen Wendepunkt, die man durch die

2. Ableitung bestimmt doch wie? (Krümmungsverhalten).

Nur Scritte würden reichen, also was ich machen soll.

Es handelt sich hier nicht um die Minima (Tiefpunkt) also wann es am kältesten ist sondern wann die Abnahme am größten ist, oder? Sonst wäre es leicht der Grafik zu entnehmen, dass es bei ca. 29 grad liegt (erster blaue Punkt also Tiefpunkt), oder?

Answer 1

Soweit ich weiß handelt es sich hier um einen Wendepunkt, die man durch die 2. Ableitung bestimmt

das ist richtig.

doch wie?

Nun - die Funktion ist gegeben. Diese muss also zweimal abgeleitet werden: $$\begin{aligned} f(x) &= 3 \sin \left( \frac{\pi}{12} (x - 11,5) \right) +33 \\ f'(x) &= \frac{\pi}{4} \cos\left( \frac{\pi}{12} (x - 11,5) \right) \\ f''(x)&= -\frac{\pi^2}{48}\sin \left( \frac{\pi}{12} (x - 11,5) \right) \end{aligned}$$dies geht mit der Kettenregel. Frage bitte nach, wenn Dir da was nicht klar ist.

Damit \(f''(x)=0\) wird, muss die Sinusfunktion zu 0 werden. Das ist der Fall, wenn das Argument ein Vielfaches von \(\pi\) ist. Also$$ \frac{\pi}{12} (x-11,5) = k \cdot \pi \quad k \in \mathbb{Z} \\ \implies x = 12 k + 11,5$$Und damit Du die Punkte mit der maximalen Abnahme (und nicht Zunahme!) findest, muss an dieser Stelle die erste Ableitung kleiner 0 (also negativ) sein \(f' \lt 0\).

Schaue Dir dazu mal die Kosinusfunktion oder besser einen Einheitskreis an. Hier nur das Ergebnis: Die Punkte maximaler Temperaturabnahme sind die mit einem ungeradem \(k\). Ersetze \(k\) durch \(k = 2n-1\) und man erhält$$x = 24n - 0,5 \quad n \in \mathbb{Z}$$ für die Zeitpunkte mit der maximalen Temperaturabnahme. Um die Temperatur zu diesem Zeitpunkt auszurechnen, muss \(x\) noch in \(f(x)\) eingesetzt werden - bzw. der Sinus sollte ja bei dieser Gelegenheit zu 0 werden ... (s.o.)

Gruß Werner