Durch die 2. Ableitung von Sinusfunktion bestimmen, wo die Änderung maximal ist, wie? T(t)= 8 . sin (pi/12(t-10,5)) +20

Question

Aufgabe:

diese Funktion soll die Änderung einer Temperatur bestimmen:

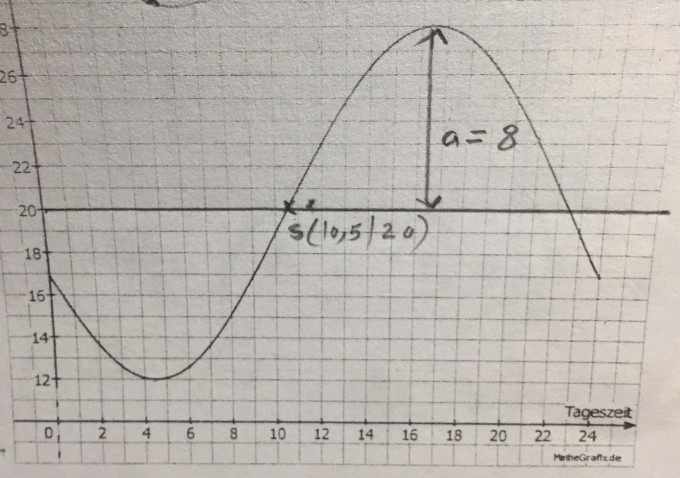
T(t)= 8 . sin (pi/12(t-10,5)) +20

dabei ist T(t) die Temperatur zum Zeitpunkt t.

Die Frage lautet:

Untersuchen Sie, bei welcher Temperatur die Temperaturabnahme  maximal ist.

Problem/Ansatz:

Soweit ich weiß, handelt es sich hier nicht um den Tiefpunkt, sonst wäre die Frage: bestimmen Sie einen Zeitpunkt, wo die Temperatur am niedrigsten ist.

Ein Kollege sagte mir, ich soll das durch die zweite Ableitung bestimmen. Irgendwas mit Wendepunkt oder so.

Ich brauche nicht unbedingt die komplette Lösung, aber würde mir jemand erklären, was ich tun soll? Bzw. Ist dann der Wendepunkt die Temperatur, bei der die Temperaturabnahme maximal ist? und müsste dann nicht 2 Wendepunkte geben? Ist es dann der Wendepunkt wo die Temperatur kalt ist?

kann man aber das nicht aus der Grafik ablesen, statt die 2. Ableitung zu bestimmen und dann den Wendepunkt?

Answer 1

Die Tempoeraturänderung wird durch die 1. Ableitung angegeben.

Du brauchst also ein Minimum ( negativer Wert mit

größtem Betrag ) der 1. Ableitung.

Das läuft auf einen Wendepunkt ( mit f ' ' (x) = 0 )

der ursprünglichen Funktion heraus.

Comments

bitte erläutern was ich als erstes machen Soll.

erste Ableitung bestimmen, dann zweite Ableitung dann gleich null setzen?

---

Stellen mit größter / geringster Änderung finden sich an den Wendepunkten.

-> 2. Ableitung null setzen und mit der hinreichenden Bedingung (3. Ableitung) überprüfen.

---

ich muss wissen, bei welcher Temperatur die Abnahme maximal ist. Ist diese Temperatur genau der Wendepunkt im Minusbereich?Also einfach die 2. Ableitung bestimmen und dann den Wendepunkt?

Müsste es dann laut der Zeichnung ungefähr (4,50 ; 12) sein, oder? also die stelle, wo die Temperaturabnahme maximal ist, ist 12?

---

f''(t)=0 setzen.

Den Wert in f'''(t) einsetzen -> Wert muss ≠ 0 sein und es muss eine rechts-links Krümmung sein (f'''(t) > 0 ), da man sonst die stärkste Zunahme berechnen würde.

Wenn die Bedingungen erfüllt sind, den Wert in f(t) einsetzen und den Funktionswert für den Punkt bestimmen.