Soll ich hier die erste und zweite Ableitung der Sinusfunktion so anwenden? Ti= 3 . sin (pi/12 (t-11,5)) +32

Question

Aufgabe:

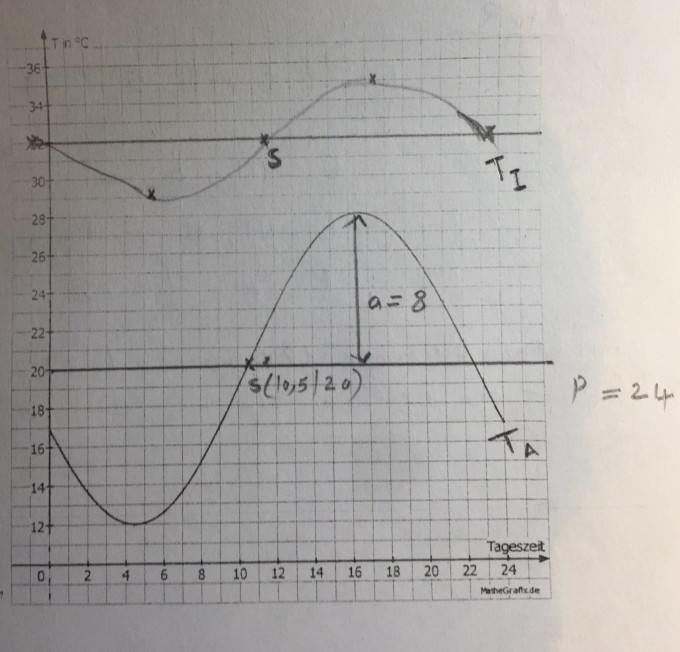
In der Zeichnung sind die Außentemperatur und Innentemperatur in einem Nest durch Kurven (Sinus Kurven) dargestellt.

(Periode ist 24h).

Funktion der Außentemperatur:

Ta(t)= 8 . sin (pi/12 (t-10,5) +20

Funktion der Innentempratur:

Ti= 3 . sin (pi/12 (t-11,5)) +32

Laut der Zeichnung gibt es eine Verzögerung im Nest, was logisch ist.

Die Aufgaben lauten:

a) bestimme die Funktion, die die Änderung der Innentemperatur im Nest beschreibt.

b) Untersuche, bei welcher Außentemperatur, die Temperaturabnahme im Nest maximal ist

Problem/Ansatz:

Zur Aufgabe 1:

Ich bestimmte einfach die 1. Ableitung von der Funktion der Innentemperatur, richtig?

Aufgabe 2 (das Problem):

Ist folgendes richtig?

Schritt 1: 2. Ableitung von Innentemperatur-Funktion bestimmen dann gleich null setzen um den Wendepunkt im negativen Bereich zu bestimmen (denn es gibt 2 Wendepunkte in einem Sinus-Funktion, oder?)

Schritt 2:

Ablesen, was dieser Punkt in der Außentemperatur-Kurve entspricht.

Ich wäre sehr dankbar für jede Antwort.

Answer 1

Hallo dein Vorgehen ist gut und richtig! etwas mehr Selbstvertrauen ist das einzige, was dir fehlt, da du ja offensichtlich das alles durchschaust? statt von Wendepunkt hättest d lieber von der maximalen negativen Änderung geredet, dh.  dem min der Funktion aus a)

Gruß lul

Comments

also welche Schritte sind jetzt für die Lösung von b da?

Sorry bin schlecht in Textaufgaben und wäre dankbar für eine Erklärung für Amateure " sozusagen

---

ist die Temperatur abnahme maximal in Minima (Tiefpunkt) ... oder Wendepunkt?

Answer 2

a) richtig

b) hier geht es um den Wendepunkt, in dem die erste Ableitung positiv ist.

Comments

Können Sie mir die Schritte schreiben als was genau soll ich am Anfang bestimmen und danach berechnen?

---

korrektur:

*also

---

Ich muss mich etwas korrigieren:

b) hier geht es um den Wendepunkt, in dem die erste Ableitung negativ ist. Und an dieser Stelle soll die Außentemperatur bestimmt werden.

Nullstellen der zweiten Ableitung von T_i(t). Die erste Ableitung an diesen Stellen bestimmen. An der Stelle t_p, wo die erste Ableitung negativ ist T_a(t_p) bestimmen.

---

ich verstehe leider nicht, was "der Wendepunkt indem die ertse Ableitung negativ ist" heißt .

Ist also Folgendes richtig:

- 2. Ableitung von Innentemperatur-Funktion gleich null setzen und den Wendepunkt bestimmen, wo die Temperaturabnahme maximal ist.

- dann Ableisen was das im Außentemperatur ist

ist das richtig?

---

Es geht um die gestrichelt gekennzeichnete Stelle t_p:

Dort ist T_i''(t_p)=0 und T_i'(t_p)<0

Gefragt ist aber nach T_a(t_p).

---

Hallo

 die Temperaturabnahme soll maximal sein, im Gegensatz zu Roland denke ich dass dazu die erste Ableitung negativ sein muss, die Temperatur soll ja fallend sein d.h, abnehmend. du suchst also das negative Maximum= minimum der ersten Ableitung, das ist der Wendepunkt auf der abfallenden Seite der ursprünglichen Kurve.

Gruß lul

---

dann müsste die Frage heißen: wann ist die Temperatur am Niedrigsten oder wann wurde die niedrigste Temperatur festgestellt, oder?

Gefragt aber denke ich, wann ist es am längsten kalt gewesen war

---

Hallo

 nein gefragt ist "Temperaturabnahme im Nest maximal"

 an der Graphik direkt kannst du das schon sehen, da wo die Temperatur am schnellsten fällt, die sin Kurve also die größte negative Steigung hat, und das ist der Fall wenn die erste Ableitung am negativsten ist, also ein Minimum hat, das hat sie , wenn die 2 te Ableitung=0 ist und die erste negativ. eigentlich sieht man es schon an der ersten Kurve , wo sie am steilsten nach unten geht.

eigentlich hattest du alles im ersten post schon richtig, wenn das "im negativen Bereich sich auf die erste Ableitung bezog.

Gruß lul