Bach Zuflussrate - Funktionsschar

Question

In ein Staubecken oberhalb eines Bergdorfes fließen zwei Bäche. Nach Regenfällen unterschiedlicher Dauer und Stärke können die momentanen Zuflussraten1 aus den beiden Bächen durch Funktionen fa für den Bach 1 und ga für den Bach 2 und die Gesamtzuflussrate aus den beiden Bächen durch eine Funktion ha für einen bestimmten Beobachtungszeitraum modelliert werden. Gegeben sind für a>0 zunächst die Funktionsgleichungen: fa(t)=14t3−3a⋅t2+9a2+340;t∈R ha(t)=14t3−7a⋅t2+24a2+740;t∈R

Dabei fasst man t als Maßzahl zur Einheit 1 h und fa(t), ga(t) sowie ha(t) als Maßzahlen zur Einheit 1m3h auf. Der Beobachtungszeitraum beginnt zum Zeitpunkt t=0 und endet zum Zeitpunkt t=6a. Die Graphen von f4, g4 und h4 sind in der Abbildung dargestellt.

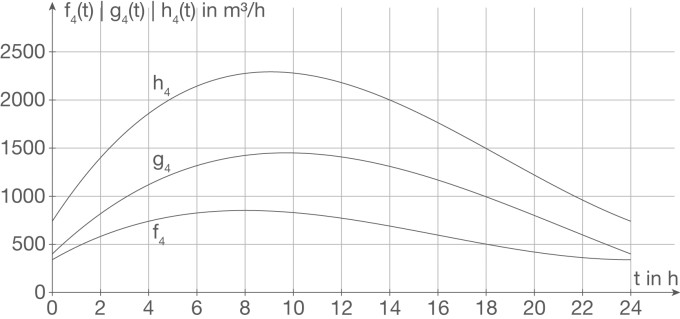
Nun frage ich mich wie folgende Aufgabe zu bearbeiten ist ->

Bestimmen Sie in Abhängigkeit von a den Zeitpunkt t∈[0; 6a ] , zu dem die Ge-
samtzuflussrate ihr Maximum annimmt.

Answer 1

Deine Funktionen passen nicht zu den Graphen. Ich bekomme eventuell für

h4(t) = 1/2·t^3 - 7·4·t^2 + 24·4^2·t + 740

den richtigen Graphen. Also bitte mal gegenprüfen.

Comments

Jo, ist nen Tippfehler. Kannst du den Rechenweg erläutern?

---

Bestimmen Sie in Abhängigkeit von a den Zeitpunkt t∈[0; 6a ] , zu dem die Ge-
samtzuflussrate ihr Maximum annimmt.

Notwendige Bedingung für ein Maximum ist das die erste Ableitung Null wird. Also bildet man die erste Ableitung und setzt diese gleich Null

ha(t) = 1/2·t^3 - 7·a·t^2 + 24·a^2·t + 740

ha'(t) = 24·a^2 - 14·a·t + 1.5·t^2 = 0 -->  t = 2.263·a