Aufgabe:
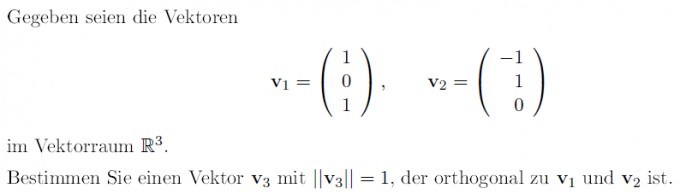
Problem/Ansatz:
nach über 2 Stunden Rumprobieren bin ich mal wieder am Verzweifeln.
Unser Prof. hat uns vieles über Orthogonalität usw. erklärt. Habe soweit alles verstanden. Formeln angewendet.
Das Problem ist aber, dass wir das immer mit Vektoren gemacht haben, die BEIDE orthogonal zueinander waren.
In der obigen Aufgabe sind v1 und v2 nicht orthogonal und die Formeln, die wir gelernt haben funktionieren da nicht.
Was tun?