es kommt ein wenig darauf an, was Du anschließend mit dieser Beschreibung machen möchtest. Eine Möglichkeit, die für viele Anwendungen (z.B. Computergraphik, Positionsberechnung, Robotik, u.a.) taugt, ist die Darstellung mit Hilfe einer Transformationsmatrix mit homogenen Koordinaten. Anbei ein kleines Beispiel
(klick auf das Bild)
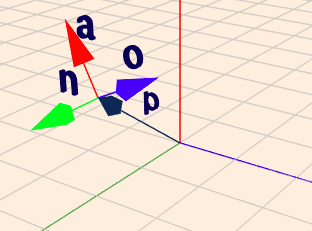
Die zugehörige Transformationsmatrix zur dargestellten Transformation auf dem Bild ist ganz konkret$$\begin{aligned} {^0}T_1 &= \begin{pmatrix} \vec{n} & \vec{o} & \vec{a} & \vec{p} \end{pmatrix} \\&= \begin{pmatrix} 1 & 0 & 0 & 3\\ 0 & 0,8 & -0,4& 1 \\ 0& 0,4 & 0,8&2 \\ 0&0&0&1 \end{pmatrix}\end{aligned}$$Die Spalten der Matrix sind die Einheitsvektoren \(\vec{n}\), \(\vec{o}\), \(\vec{a}\) und die Position \(\vec{p}\) des neuen Koordinatensystems (1) im Bezugssystem (0). Der Vorteil liegt darin, dass man durch Hinzufügen einer Dimension aus einer affinen Abbildung eine lineare Abbildung macht. So kann man dann aus einer Koordinate \({^1p}\), die im 1-System gegeben ist, durch einfache Matrix-Vektor-Multiplikation die Koordinate \({^0p}\) im 0-System berechnen$${^0p} = {^0T}_1 \cdot {^1p}$$Die vierte Koordinate von Positionen ist immer =1. Und nach dem Invertieren der Matrix geht es auch umgekehrt. Und man kann diese Matrizen auch kombinieren - wie hier gezeigt wird.