Kreisteile: Schraffierte Fläche berechnen

Question

Welchen Ansatz kann ich bei dieser Aufgabe wählen?

Aufgabe:

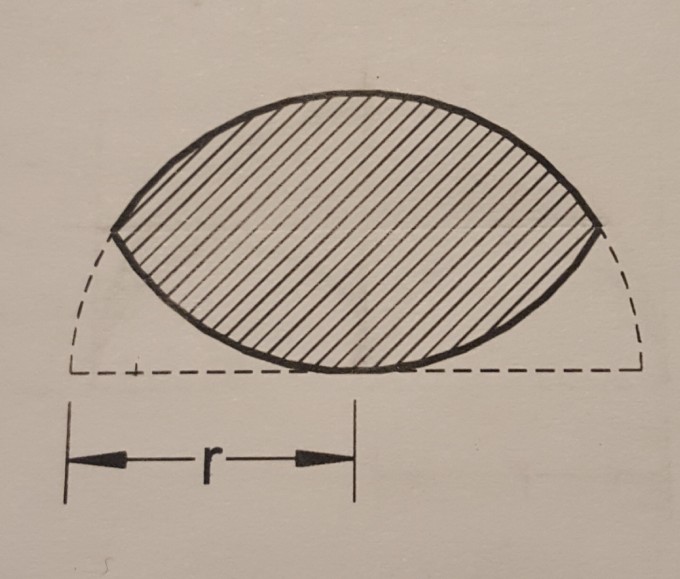
Ich muss die schraffierte Fläche berechnen.

Problem/Ansatz:

Es tut mir leid, dass ich des öfteren nachfrage, aber ich schaffe diese Aufgabe einfach nicht. Mir fehlt der Ansatz.

Wie kann ich es schaffen, dass ich solche Aufgaben selber lösen kann? Wie kann ich Schritt für Schritt vorgehen, um sowas zu lösen? Und ist das normal, dass ich immer nie einen Ansatz bei solchen schwierigen Aufgaben finde? Woran könnte es liegen?

Comments

Ich möchte nicht, dass mir jemand die Lösung hinschreibt. Ich möchte die Gedankengänge nachvollziehen und jeden einzelnen Schritt selber machen. Könnte jemand so etwas mit mir machen?

---

Ich habe bis jetzt das entdeckt. Könnte sich jemand das anschauen und mir sagen, ob ich auf der richtigen Spur bin, aber bitte nur kleine Tipps geben und nicht die Lösung sagen.

---

omg, ich habe es geschafft mit meinem Ansatz.

---

Könnt ihr euch vielleicht meinen Lösungsweg anschauen und sagen, ob ich das so gut gemacht habe oder ob man da anders rangehen sollte. Vielleicht hatte ich einfach Glück. Durch das Einzeichnen des Dreiecks habe ich gesehen, dass dieses Kreissegment oben berechnet werden kann und einfach verdoppelt werden kann.

---

ich kann dir zwar nicht weiterhelfen wollte aber aus Interesse fragen wie du von $$\frac{2}{3}\pi \cdot r^2 - \frac{\sqrt{3}}{2} \cdot r^2 \quad \mid \sqrt{}$$
$$ \frac{4 \ \pi \cdot r^2 - 3\sqrt{3}\ r^2}{6} \quad \mid \sqrt{}$$ auf gekommen bist, also wie kommst du von 2/3 * pi auf einmal auf 4*pi und wie kommst du von -\frac{\sqrt{3}}{2} * r^2 auf -3 * \sqrt{3} *r^2 kommst.. Wäre cool wenn du diesen Rechenschritt von dir erklären könntest.

---

Ich habe auf den Hauptnenner 6 erweitert.

Von der drei auf die Sechs ist mal 2. Also nehme ich den ganzen Zähler mal zwei.

(2*(2*pi*r^2))/6

Von der zwei auf die Sechs ist mal 3. Also nehme ich den ganzen rechten Zähler mal drei.

(3*(Wurzelaus3 * r^2)/6

Dann nehme ich die Differenz.

(4*pi*r^2 - 3Wurzel3 * r^2)/6

Und dann kannst du noch r^2 und 1/6 ausklammern.

Answer 1

Berechne zunächst die Fläche A des gleichseitigen Dreiecks im Bild 3.

Bild 1:                                              Bild 2                                            Bild 3

Und dann den Sechstelkreis S in Bild 2. Und dann die graue Fläche C=S-A in Bild 3. Die gesuchte Fläche ist dann 2A+4C.

Answer 2

Dein Ergebnis ist korrekt.

Vielleicht hatte ich einfach Glück.

Der Fachbegriff dafür ist Intuition.