Über Relationen, den Flächeninhalt bestimmen? (Ähnlichkeit, Dreieck)

Question

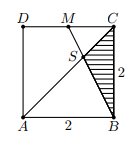
der Flächeninhalt der schraffierten Fläche beträgt 2/3. Ich erinnere mich daran, dass z. B. Werner-Salomon, Gast hj2166 et al. solche Aufgaben mit irgendwelchen Beziehungen gelöst haben.

Beziehungsweise nicht, wie ich zwei Geradengleichungen AC und BM aufgestellt, deren Schnittpunkt S berechnet, dann alle Seitenlängen (SC und SB) berechnet und dann mit heronischen Flächenformel den Flächeninhalt bestimmt.

Ich meine, sie haben sich auf die Ähnlichkeit der Dreiecke bezogen. Vor allem freuen würde ich mich über weiterführende Links... Ich weiß nicht genau, wie ich danach suchen soll.

Answer 1

AB : MC = 2:1        | 2. Strahlensatz (Zentrum S) 

==> AS : SC = 2:1

D.h. SC = 1/3 AC.

==> Im schraffierten Dreieck gilt wegen 1. Strahlensatz (Zentrum A):  h_(BC) = 1/3 * 2 = 2/3

A_Dreieck = 1/2 * 2/3 * 2 = 2/3

Comments

Hallo TR,

dass AB : MC = 2:1 ist, ist gut nachzuvollziehen. Was ist aber mit

AC : SC = 2:1

Woran machst du fest, wie lang die Diagonale ist? Oder Warum AC = 2 und SC =1?

---

Es geht nur um Verhältnisse.

Oder Warum AC = 2 und SC =1? 

ist eine falsche Folgerung.

Ich habe angeschrieben, welchen Strahlensatz ich benutze. Jeweilige Zentren gerade noch ergänzt. Für den 1. Teil (Zentrum S) ist die Figur vollständig. Für den zweiten Teil (Zentrum A) kannst du durch S noch eine Parallele zu BC dazudenken.

---

Und wie folgerst du daraus, dass SC=1/3 AC

---

mmh?

Beispiel:

8 : 4 = 2 : 1

4 = 1/3 * (8+4) = 1/3 * 12

---

Ich kann folgende Beziehungen aufstellen:

SA/SB=SD/SC , SA/SC=SB/SD

AB/DC=SB/SD , AB/DC=SA/SC

und weiß, dass AB=2 und DC=1

wie man nun daraus SC= 1/3 AC folgern soll, ist mir immer noch nicht klar.

---

AS + SC = AC .

---

Bingo! Jetzt hat's Klick gemacht.

---

Gut. Freut mich!

---

Wie kann ich notieren, dass z. B. im kleineren Dreieck alle Längen im Verhältnis 2:1 zu dem großen Dreieck stehen?

Mit der Tilde?

Answer 2

Das ganze ist doch ein Quadrat 2x2 hat also Fläche 4.

Die Hälfte also 2 und weil das rechte Stück 2/3 ist, ist also das untere

Dreieck  4/3.

Seine Grundseite ist 2, also seine Höhe ist 4/3 .

Und damit hat das obere Dreieck die Höhe 2/3 und die

Grundseite 1 , also Fläche 1/3.

Damit hat das 4-eck die Fläche  5/3.

Comments

Man weiß nicht von Grund auf, dass die schraffierte Fläche 2/3 ist: Das ist zu berechnen.