Wo ist der Fehler in folgender Argumentation über Relationen

Question

Ich soll zeigen, wo in dieser Argumentation der Fehler liegt

Die Aufgabe ist aus 2020 und ich finde leider keine Lösung dazu… deshalb wäre ich für jede Hilfe sehr dankbar !

Text erkannt:

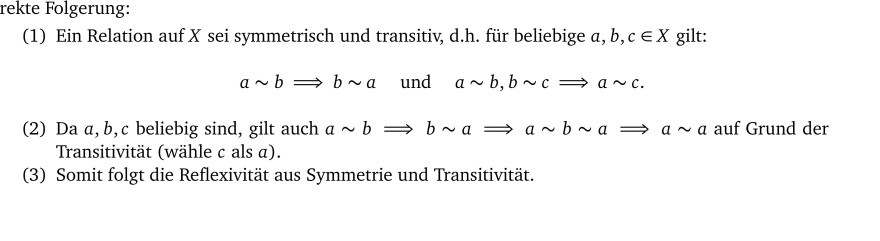
rekte Folgerung:
(1) Ein Relation auf \( X \) sei symmetrisch und transitiv, d.h. für beliebige \( a, b, c \in X \) gilt:
\( a \sim b \Longrightarrow b \sim a \text { und } a \sim b, b \sim c \Longrightarrow a \sim c . \)
(2) Da \( a, b, c \) beliebig sind, gilt auch \( a \sim b \Longrightarrow b \sim a \Longrightarrow a \sim b \sim a \Longrightarrow a \sim a \) auf Grund der Transitivität (wähle \( c \) als \( a \) ).
(3) Somit folgt die Reflexivität aus Symmetrie und Transitivität.

…

Problem/Ansatz:

Meine Vermutung ist, dass es etwas damit zu tun hat, dass  a~b , b~c => a~c nicht das gleiche wie a~b~c => a~c

Oder es hat etwas damit zu tun, dass man für c nicht einfach a verwenden darf.

Answer 1

Eine Aussage der Form

        \(A \implies B\)

bedeutet

        Wenn \(A\) gilt, dann gilt auch \(B\).

Insbesondere bedeutet sie nicht

        Es gilt \(A\), deshalb gilt auch \(B\).

Um mittels \(A \implies B\) zu begründen, dass \(B\) gilt, muss man deshalb begründen, warum \(A\) gilt.

\( a \sim b \implies b \sim a \implies a \sim b \sim a \implies a \sim a \)

Damit ist bewiesen:

        Wenn \(a \sim b\) gilt, dann gilt auch \(a\sim a\).

Zu beweisen ist aber:

        Es gilt \(a\sim a\).

Comments

Also das heißt, dass a~a nur unter der Bedingung gilt, dass a~b steht? Das ist ja hier nicht unbedingt immer der Fall, da nicht von einer totalen Ordnung die Rede ist, richtig? Wenn ich also ein a und ein b finde, für das nicht gilt: a~b gilt, gilt nach der Argumentation oben auch nicht a~a, richtig?

Wenn allerdings eine totale Ordnung gegeben wäre, wäre die Argumentation richtig weil für alle Elemente a~b und b~a („und“ weil es ja eine Symmetrie vorhanden ist ) gelten würde, oder?

---

Wenn ich also ein a und ein b finde, für das nicht gilt: a~b gilt, gilt nach der Argumentation oben auch nicht a~a, richtig?

Falsch.

Wenn du ein \(a\) hast, dann genügt es, ein \(b\) mit \(a\sim b\) zu finden, um mittels Symmetrie und Transitivität \(a\sim a\) nachzuweisen.

Beispiel. \(a\sim b \iff \exists z\in \mathbb{Z}:\ 2z = a-b\)

Symmtrie: \(a\sim b\implies 2z = a-b\implies 2\cdot (-z)=b-a\implies b\sim a\).

Transitivität: \(a\sim b\wedge b\sim c \implies 2z_1 = a-b\wedge 2z_2=b-c\implies 2\cdot (z_1+z_2)=a-c\implies a\sim c\).

Es gilt zwar nicht \(3\sim 8\), aber es gilt \(3\sim 17\). Mit Symmetrie und Transitivität folgt daraus \(3\sim 3\).