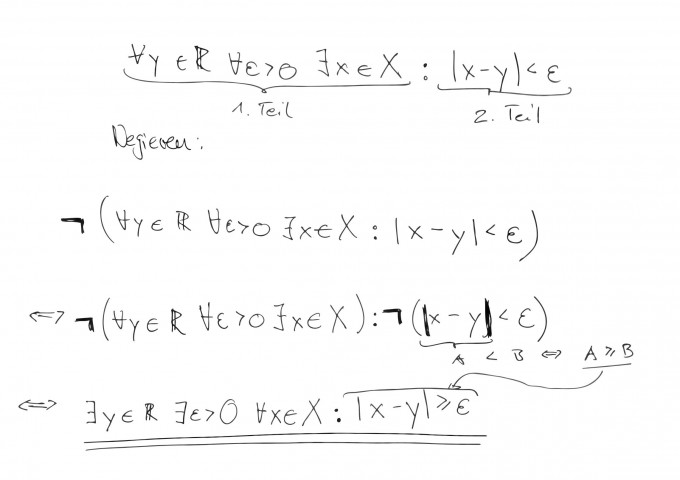Danke Wolfgang !
Ich habe eine Pause gemacht und selbst überlegt, vielleicht kannst du noch etwas dazu sagen:
Eine logische Aussage besteht ja (fast) immer im einfachen Fall aus zwei teilen.
Der vordere Teil nennt sich (glaube ich) der Teil der die Aussage quantifiziert, und der hintere teil, also die Eigenschaft ist die Eigenschaft die über die quantifizierten Objekte oder Elemente getroffen wird.
Nun haben wir eine Aussage gegeben:
Und ich muss die Gesamtaussage negieren.
Ich gehe so vor:
Ich Teile die Aussage in zwei bis zum ":" Doppelpunkt wo die Eigenschaft anfängt.
Im vorderen Teil, also bei der Quantifizierung, werden die Quantoren umgedreht.
Im zweiten Teil, dort wo die Eigenschaft anfängt gibt es andere Umformungsregeln.
Eben die, die du mir rechts von der Negation notiert hast.
Also im Allgemeinen will ich sagen, dass ich in der Pause und mit deiner Hilfe verstanden habe wie man prinzipiell Aussagen negiert.
Ich fasse nochmal zusammen:
1. Eine Aussage ist gegeben.
2. Ich setze Klammern über die Gesamtaussage mit einem Negationszeichen davor.
3. Ich setze Klammern um den Ersten Teil, und setze Klammern um den zweiten Teil.
4. Ich negiere den ersten Teil: Quantoren vertauschen.
5. Ich negiere den zweiten Teil: Deine Regeln anwenden.
Frage:
(1) Was sagst du zu dem was ich sage?
(2) Ich nehme an, dass die Relationen im zweiten Teil gegenteilige Wahrheitswerte in einer Wahrheitstafel haben. Ohne für jedes einzelne die Wahrheitstafel aufzustellen, wo finde ich diese Umformungsregeln ? Ich glaube wir haben das in einer Zusammenfassung dort gibt es Regeln wie De Morgan'sche Gesetze etc...
Angewendet: