Bogenlänge hyperbolischer Kosinus f(x) = cosh(x/7)

Question

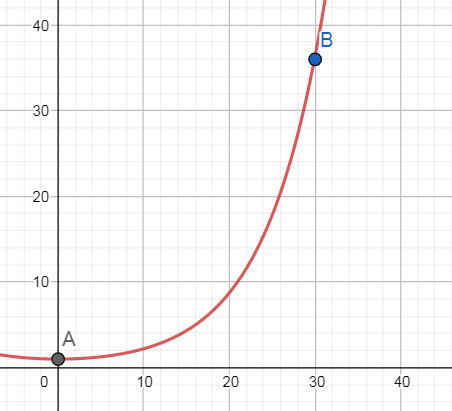
ich möchte die Seillänge mittels hyperbolischen Kosinus berechnen. Die Bogenform soll ähnlich der in der angefügten Grafik sein, also durch zwei Punkte gehen, die folgende relative Koordinaten zueinander haben: (dx=30; dy=35). Das habe ich mit der Funktion f(x) = cosh(x/7) realisiert. Jetzt möchte ich die Bogenlänge im Intervall [0; 30] berechnen.

Die Bogenlänge berechne ich mit s=\( \int\limits_{0}^{30} \)\( \sqrt{1+(y')²} \)*dx, meine Ableitung ist 1/7*sinh(x/7). Ich komme als Ergebnis aber immer auf gerundete 105. Das ist m.E. deutlich zu hoch - wo liegt mein Fehler?

Answer 1

Ich komme auf:

\( \displaystyle\int\limits_0^{30}\sqrt{1+\left(\dfrac{1}{7}\sinh\left(\dfrac{x}{7}\right)\right )^2}=\int\limits_0^{30}\sqrt{1+\dfrac{1}{49}\sinh^2\left(\dfrac{x}{7}\right)}\approx 51.87 \).

Deine Ableitung stimmt auch. Vielleicht Klammern vergessen?

Answer 2

ich habe erhalten:

≈ 51. 87

aber mit elementaren Mitteln läßt sich das Integral nicht lösen.