Abstandsberechnung nur in eine Richtung.

Question

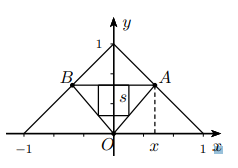
wenn ich die Punkte A(x|1-x) und P(x|0), wie kann ich dann auch wirklich diejenige Strecke berechnen, die im Bild zu sehen ist.

d²=(x-x)²+(0-(1-x))²

ist dann was "anderes" als:

d²=(x-x)²+(1-x-0)²

Mir ist bewusst, dass nach dem Wurzelziehen ± davor steht, aber was, wenn ich nur die eine Lösung suche.

Comments

Die Strecke d, um die es wohl geht, ist in der Skizze nicht bezeichnet.

d²=(x-x)²+(0-(1-x))² gibt hier keinen Aufschluss, zumal x-x=0 und d=1-x.

Dann wäre d der Term der Geraden durch (0|1) und (1|0).

Answer 1

Hallo

1. d ist immer positiv.

2. der Abstand AP und der Abstand PA sind doch dasselbe, auch wenn du deine Rechnung ansiehst.

Gruß lul

Comments

Die Höhe des Dreiecks ABO ist gesucht. Diese ist h=1-x

---

Okay, habe es herausgefunden. Beim Verbindungsvektor kann man die Richtung auswählen. Ich berechne einfach \(\overrightarrow{PA}=\overrightarrow{a}-\overrightarrow{p}\). Dann kann ich auch die Wurzel ziehen, weil der Abstand, da er in die positive Richtung der Ordinante im ersten Quadranten führt, stets positiv ist.

\(\sqrt{(1-x)^2}=1-x\)