Anwendung der Integralrechnung

Question

Aufgabe:

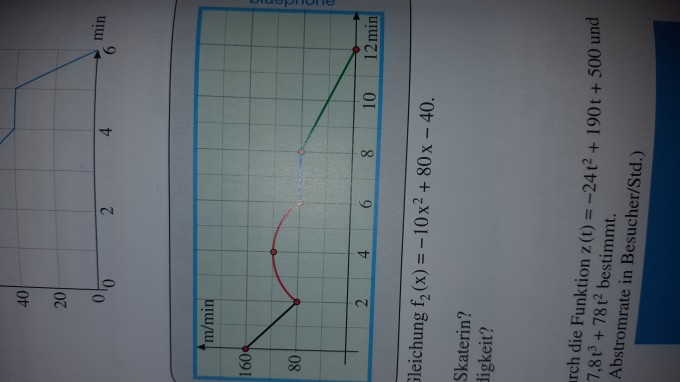
Eine Skaterin läuft ihr Trainingsprogramm ab, welches ihr die auf dem Smartphone dargestellte Geschwindigkeitskurve vorgibt. Diese Kurve besteht aus vier Teilfunktionen.

a) Bestimmen Sie die Gleichungen der drei linearen Teilfunktionen f₁ , f₃ und f₄ . Geben Sie jeweils auch deren Definitionsintervalle an.

b) Die quadratische Teilfunktion f₂ hat die Gleichung f₂(x) = -10x^2 + 80x - 40. Bestätigen Sie dies.

c) Wie lang ist die gesamte Laufstrecke der Skaterin?

d) Wie groß ist ihre Durchschnittsgeschwindigkeit?

Könnte zunächst jemand meine Ergebnisse kontrollieren?

Bei d) habe ich leider gar keinen Ansatz. Muss ich da mit dem Mittelwertsatz arbeiten?

Answer 1

Das könnte wie folgt aussehen:

a) Bestimmen Sie die Gleichungen der drei linearen Teilfunktionen f1 , f3 und f4 . Geben Sie jeweils auch deren Definitionsintervalle an.

f1(x) = 160 - 40·x ; 0 ≤ x < 2
f3(x) = 80 ; 6 ≤ x < 8
f4(x) = 80 - 20·(x - 8) ; 8 ≤ x ≤ 12

b) Die quadratische Teilfunktion f2 hat die Gleichung f2(x) = -10·x^2 + 80·x - 40. Bestätigen Sie dies.

f2(2) = -10·2^2 + 80·2 - 40 = 80
f2(4) = -10·4^2 + 80·4 - 40 = 120
f2(6) = -10·6^2 + 80·6 - 40 = 80

c) Wie lang ist die gesamte Laufstrecke der Skaterin?

A1 = ∫ (0 bis 2) f(x) dx = 1/2·(160 + 80)·2 = 240 m
A2 = ∫ (2 bis 6) f(x) dx = (-10/3·6^3 + 40·6^2 - 40·6) - (-10/3·2^3 + 40·2^2 - 40·2) = 426 2/3 m
A3 = ∫ (6 bis 8) f(x) dx = 80·2 = 160 m
A4 = ∫ (8 bis 12) f(x) dx = 1/2·80·4 = 160 m
A = 240 + 426 2/3 + 160 + 160 = 986 2/3 m

d) Wie groß ist ihre Durchschnittsgeschwindigkeit?

v = s/t = (986 2/3)/12 = 82 2/9 m/s

Comments

Vielen Dank!

Hätte man es bei b auch so wie ich machen können?

Ist meine Notationsvariante für die Definitionsintervalle in Ordnung, oder inkorrekt?

---

Doch. Das darfst du so machen. Aber wenn du etwas bestätigen sollst dann darfst du das was du bestätigen willst in der Rechnung benutzen. Daher ist meine Version nur deutlich einfacher.