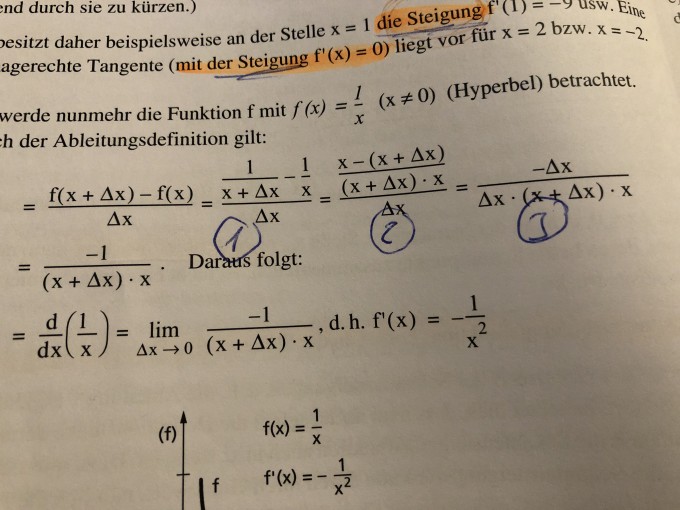Umstellen der Herleitung einer Ableitung

Question

Aufgabe:

Umstellen einer Ableitungsdefinition siehe Anhang

Problem/Ansatz:

Hallo ihr Matheexperten :)

ich versuche, mich derzeit mit der Ableitungsdefinition mittels Differenzialquotient anzufreunden (was soweit auch klappt). Dabei tue ich mir extrem schwer beim Umstellen der Gleichung siehe Anhang. Speziell verstehe ich in der Lösung die Vorgehensweise von 1 auf 2 und zwei auf 3 nicht. Für eine detaillierte Erklärung wäre ich sehr dankbar..

Kevin

Answer 1

von 1 zu 2 : wurde der Hauptnenner gebildet

von 2 zu 3:

x-(x+deltax)=  - delta x

dann wurde der Doppelbruch beseitigt:

allgemein gilt:

(a/b) / (c/d) = (a d)/(b c)

d ist in diesem Fall 1

Comments

Vielen Dank für deiner/ eure Antworten. Ich habe versucht siehe Anhang den Hauptnenner zu bilden und daraus den Zähler zu berechnen.. leider nur teilweise erfolgreich. Wo genau habe ich mich verrechnet?

Ich verstehe trotz deiner Erklärung noch nicht genau, wie ich den Doppelbruch mit dieser Methode umschreibe..

Danke vorab für die Bemühungen

Answer 2

Der Übergang von 2 nach 3 ist reine Bruchrechnung: Ein Bruch wird durch Δx (oder jeden anderenTerm) geteilt, indem man den Nenner mit Δx multipliziert.

Der Übergang von 1 nach 2 ist ebenfalls reine Bruchrechnung: Brüche werden subtrahiert, indem man sie zunächst auf den Hauptnenner (hier (x+Δx)·x ) erweitert.