Na ja, das kommt darauf an von wo aus man draufschaut. Die Punkte bleiben ja da wo sie sind - nur das Koordinatensystem wechselt...
Deine Ebene liegt schräg. Ich hab mal eine orthonormal Basis aus den Vektoren gemacht. Die Ebene lautet dann auf
\(\small Ev(r, s) \, := \, \left( \begin{array}{r}0.958 \; r + 0.089 \; s\\-0.951 \; s\\ -0.287 \; r + 0.297 \; s\\ \end{array} \right) \)
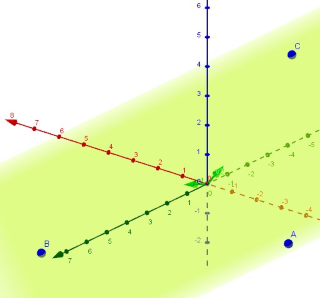
v1 normiert und v2 rechtwinklig dazu gewählt.
Damit heißt die Transformationsmatrix
\(T \, := \, \left(\begin{array}{rrr}0.958&0&-0.287\\0.089&-0.951&0.297\\\end{array}\right)\)
und die Koordinaten von A in der Ebene E lauten dann
\(T A \, := A_v = \, \left(-5.939, -3.506 \right)\)