Hi !
ich treffe Schwierigkeiten mit den Grenzen für ein Volumenintegral. Wie der Verlauf bei solcher Integration ist , kenne ich schon meine Probleme liegen einfach an der Auswahl der Grenzen
z.b Hier
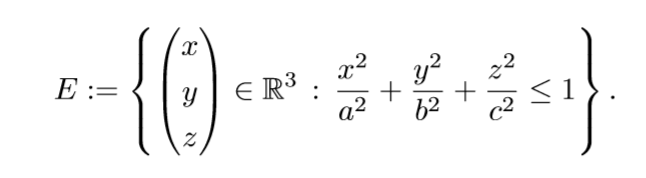
muss ich das Volumen des Ellipsoids E berechnen , wobei a,b,c größer 0 sind . Ich habe keine Ahnung wie ich die Grenzen auswählen kann/soll !
Könnte mir jemand sagen wie man die Grenzen im allgemeinen und auch in diesem Beispiel auswählen kann ?
Vielen vielen Dank im voraus !