Du könntest Dir zunächst eine Skizze machen. Zeichen die drei Punkte \(A\), \(P\) und \(Q\) ein und ziehe durch \(A\) eine Gerade mit der Steigung \(m=2/3\):
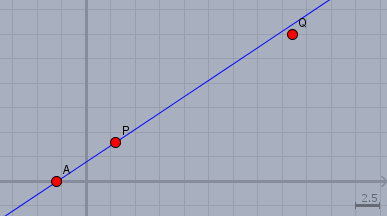
Dann sieht man schon, dass \(Q\) nicht auf der Geraden liegt, aber \(P\) anscheinend schon.
Habe jetzt folgendes gemacht:
y = 2/3x + q
das heißt y = 2/3x + 2
das ist richtig, das ist die Gleichung für die gegebene Gerade durch \(A\).
Dann habe ich y = 11/18x + q ...
das ergibt keinen Sinn. \(11/18\) ist die Steigung der Geraden durch die Punkte \(P\) und \(Q\). Aber warum sollte diese Gerade hier irgendeine Rolle spielen? Schau in die Skizze oben. Es ist doch nur gefragt, ob die beiden Punkte \(P\) und \(Q\) auf der Geraden durch \(A\) liegen.
Setze dazu die X-Koordinate der Punkte in die Geradengleichung ein: $$P: \space x_P = 3, \space y_P = 4 \\ \frac 23 x_p + 2 = \frac 23 \cdot 3 + 2 = 4 = y_P$$also liegt \(P\) auf der Geraden. Das Paar \((3|4)\) erfüllt die Geradengleichung. $$Q: \space x_Q= 21, \space y_Q= 15 \\ \frac 23 x_Q + 2 = \frac 23 \cdot 21 + 2 = 16 \ne y_Q$$ \(Q\) liegt also nicht auf der Geraden.
Frage bitte nach, falls noch irgendwas unklar ist.
Gruß Werner