Hallo Mary,
Du solltest Dir immer eine Skizze machen:
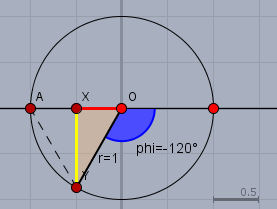
Zeichnet man die 120° in den (Einheits)kreis so kann man das gleichseitige Dreieck \(\triangle YOA\) einzeichnen. In diesem Dreieck sind alle Seiten gleich lang und alle Winkel betragen 60°. Und 60° ist der Nebenwinkel zu 120° hier aus der Aufgabe.
Die Werte für den Sinus (gelb) und den Cosinus (rot) kann man mehr oder weniger aus der Skizze ablesen. Da die Linie durch \(XY\) das gleichseitige Dreieck halbiert, ist \(|XO|=1/2\) (Bem.: hier ist \(r=1\)) Und \(|XY|\) berechnet sich nach Pythagoras:$$|XY|^2 + |XO|^2 = 1 \implies |XY| = \frac 12 \sqrt 3$$Jetzt achte noch auf die Vorzeichen - nach unten und nach links sind die Längen negativ zu zählen - also ist:$$\sin (-120°) = -|XY| = -\frac 12 \sqrt 3 \\ \cos(-120°) =- |XO| = -\frac 12$$Und der Tangens ist das Verhältnis von Sinus zu Cosinus:$$\tan (-120°) = \frac {\sin(-120°)}{\cos(-120°)} = \frac{-|XY|}{-|XO|} = \sqrt 3$$
Vielleicht fällt Dir jetzt auf, dass bei Deinen Aufgabe immer dieses halbe gleichseitige Dreieck vorkommt!
Wie berechnet man einen Winkel mit einem Punkt aus dem Koordinatensystem?
hier liegt es so:

Wie bestimmt man Polarkoordinaten und was sind die überhaupt?
und hier liegt es so:
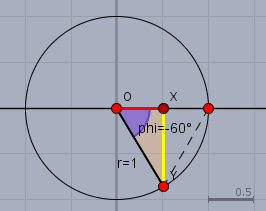
es ist also immer das gleiche Dreieck. Und die Aufgaben lassen sich alle auf die selbe Art und Weise mit Kenntnis über diese Dreieck lösen.
Gruß Werner