... weiss ich überhaupt nicht wie ich diese Aufgabe angehen soll.
Schau Dir doch mal dieses Bild an (draufklicken und Szene drehen)
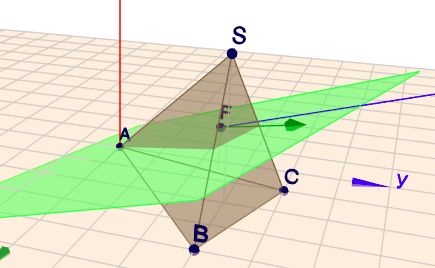
Welche Punkte musst Du bestimmen um Deine Aufgabe zu lösen?
Fortsetzung:
Ja die kann ich sehen, wenn ich das Bild von der Seite sehe.
Die Pyramide von der Seite sieht so aus:
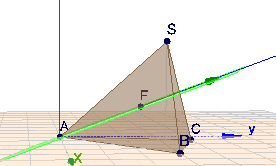
ich sehe da keine Fläche; eher einen Strich. Von oben ...
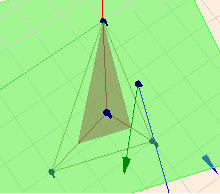
... kann man das Stück der Pyramide sehen, was aus der Ebene heraus ragt. Die Schnittfläche ist ein Dreieck. Und von unten ...
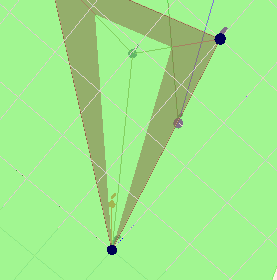
... sieht man das Dreieck noch besser. Diesmal als das Stück der Ebene, was sich im Inneren der Pyramide befindet.
Ich habe den oberen Teil der Pyramide etwas angehoben und die Schnittfläche rot eingefärbt, so kannst Du sie besser sehen:
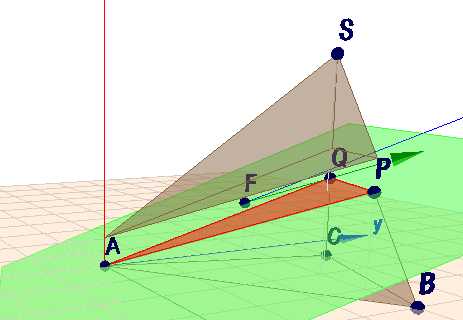
(dieses Bild ist wieder zum drauf klicken und drehen)
Gefragt ist nach dem Umfang der Fläche, also dieses Dreiecks. Und dafür benötigt man die Eckpunkte des Dreiecks. Und das sind die Punkte, wo sich die Kanten \(AS\), \(BS\) und \(CS\) mit der Ebene schneiden - so wie es Woodoo bereits vorgeschlagen hat.
Die drei Eckpunkte sind \(A\), \(P\) und \(Q\) mit den Koordinaten $$P=\begin{pmatrix} 6\\6\\3 \end{pmatrix}, \quad Q= \begin{pmatrix} 3\\7\\3 \end{pmatrix}$$Das Dreieck hat den Umfang \(U\) von$$U= |AP| + |PQ| + |QA| = 9 + \sqrt{10}+ \sqrt{67} \approx 20,35$$Falls Du Fragen hast, wie man den Schnittpunkt von Gerade und Ebene berechnet oder die Abstände zwischen zwei Punkten, so melde Dich bitte.
Gruß Werner