Parabelförmige Hochspannungsleitung zwischen Punkt A (0/0) und B (100/20)

Question

Aufgabe:

Eine Hochspannungsleitung hängt zwischen den Punkten A und B näherungsweise parabelförmig durch . Der Punkt B ist von A (0/0) in horizontaler Richtung 100m entfernt und liegt 20m höher als A. Der tiefste Punkt C der Parabel p ist von A in horizontaler Richtung 20m entfernt

A- Gib die Gleichung der Parabel p in der Scheitelpunktform, der allgemeinen Form und der Produktform an.

B-stelle einen Term h(x) für den Durchhang h auf, fine heraus , an welcher Stelle der Durchhang am größten ist, und und ermittle hmax

Problem/Ansatz:

Answer 1

Hallo

 kennst du denn die Scheitelform? und du weisst der Scheitel liegt bei x=20, dann hast du in der Scheitelform 2 Unbekannte, setze  (0,0) und (100,20) ein und bestimme daraus die 2 Unbekannten, Daraus kannst du dann hoffentlich die anderen formen hinschreiben?

mit Durchhang ist wohl der  vertikale Abstand von der Geraden zwischen A und B gemeint.

Gruß lul

Answer 2

die allgemeine Scheitelpunktform einer Parabel lautet

f(x)=a(x-d)^2 + e

Der Scheitelpunkt hat somit die Koordinaten (d|e), in diesem Fall (20|?)

Du hast die Koordinaten zweier Punkte.

A (0/0)

$$⇒a(0-20)^2+e=0$$

$$⇒e=-400a$$

Punkt B ist von A (0/0) in horizontaler Richtung 100m entfernt und liegt 20m höher als A

$$B(100|20)$$

$$⇒a(100-20)^2+e=20$$

$$e=20-6400a$$

Daraus ergibt sich

$$-400a=20-6400a$$

$$⇔a=\frac{1}{300}$$

Damit ist e =- \( \frac{4}{3} \)

und somit lautet die Gleichung in der Scheitelpunktform

$$f(x) = \frac{1}{300}(x-20)^2-\frac{4}{3}$$

Damit kannst du (hoffentlich) auch die anderen beiden Formen bilden.

Gruß, Silvia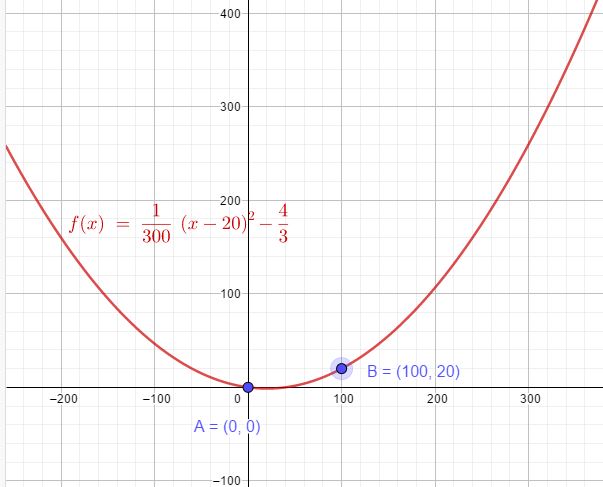

,

Comments

Und wie geht weiter ? Bitte

---

Für die allgemeine Form gilt es nun die scheitelpunktsform mit Hilfe der binomischen Formel auszumultiplizieren.

f(x)=1/300*(x-20)^2-4/3

  =1/300*(x^2-40x+400)-4/3

   = 1/300*x^2-4/30*x+400/300-4/3

    = 1/300*x^2-4/30*x