Volumen einer Fläche wenn man sie um die x- Achse rotieren lässt

Question

Hallo:)

Ich hoffe Ihr könnt mir bei dieser Aufgabe helfen.

Danke schon mal:)

Die Funktion f(x)= e^(1-x), die Tangente an die Funktion im Schnittpunkt mit der y-Achse, die Gerade x=2 und die x-Achse schließen die Fläche F ein. Berechne das Volumen das entsteht, wenn man diese Fläche um die x-Achse rotieren lässt.

Answer 1

Stelle die Funktionsgleichung für das Flächenstück auf (Integral).

Weiteres findest du hier:

https://www.frustfrei-lernen.de/mathematik/rotationsvolumen-volumen-rotationskoerper

Answer 2

der Schnittpunkt mit der \(y\)-Achse ist bei \(x_0=0\) zu finden. Die Tangente berechnet sich aus:$$t(x)=f'(x_0)(x-x_0)+f(x_0)$$

Berechne nun \(V=\pi\cdot \int_{0}^{2}(f(x))^2 \text{ dx}\) und ziehe \(\pi\cdot \int_{0}^{1}(t(x))^2 \text{ dx}\) ab.

Comments

Wie macht man das ?

---

Welchen Schritt meinst du?

---

Als das Subtrahieren einer Fläche von einem Volumen dran war, muss ich wohl gefehlt haben.

---

Stimmt, man sollte wohl besser \(\pi\cdot \int_{0}^{1}(t(x))^2 \text{ dx}\) subtrahieren.

Answer 3

Handelt es sich um die schraffierte Fläche

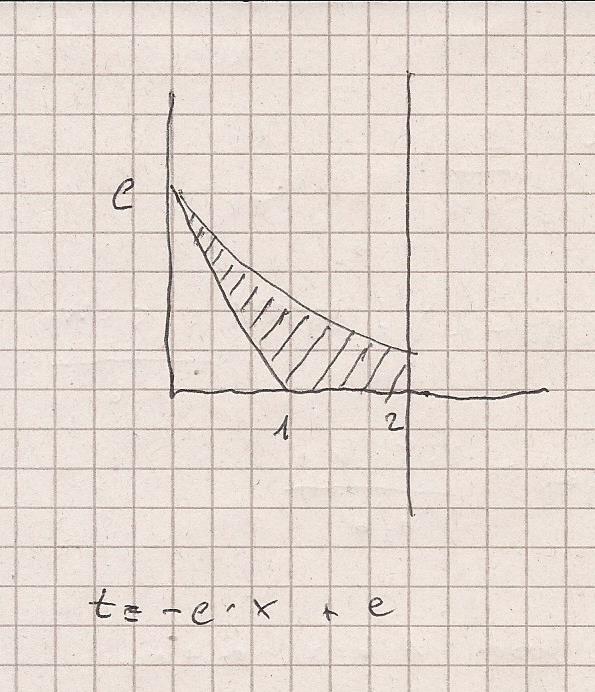
Die Tangente ist  t ( x ) = -e * x + e

2 Volumina getrennt ausrechnen
f ( x ) =... ( zugleich Radius )
A ( x ) = π *  [ f ( x ) ] ^2
V ( x ) = ∫ A ( x ) dx zwischen x = 0 und x = 2

Dreieck Tangente
t ( x ) = ... ( zugleich Radius )
A ( x ) = π *  [ t ( x ) ] ^2
1 ist der Nullpunkt von t
V ( x ) = ∫ A ( x ) dx zwischen x = 0 und x = 1

Volumen = Volumen 1 minus Volumen 2

Bei Bedarf nachfragen.

Comments

Vielen lieben danke!:)

Dann wäre das Ergebnis also 7,737... könnte das stimmen?

---

7.737 ist das Volumen des Körpers
unterhalb der Tangente.
Das Volumen unterhalb der Kurve ist
11.394

---

Das Volumen 2 (Kegel) erhält man auch ohne Integral:

 V₂ = 1/3 · π · r² · h = 1/3 · π · e² · 1 =  πe² / 3