Tangentengleichung der natürlichen Exponentialfunktion

Question

ich habe eine Frage an euch. Also die aufgabe heißt :

Bestimmen Sie die Gleichung der Tangente an den Graphen der natürlichen Exponentialfunktion in den Punkt A ( 1 /e ) und B ( -1 / e^ -1)

meine Lösung :

Tangentengleichung : t(x)= mx+b

Steigung m : Habe ich mit der ersten ableitung berechnet . f ( 1) = e^1 = e

Berechnung von b : e^-1=e^-1x (-1) +b dem nach ist b = 2e^-1

Tangentengleichung ist t(x)=ex+2e^-1

IST DAS RICHTIG ???

Ich soll noch rausfinden in welchen Punkt schneidet die Tangente die x-Achse und y-Achse ? Muss ich das Zeichne und gucken oder kann ich das rechnerisch auch rausfinden?

 

Answer 1

f(x) = e^x
f'(x) = e^x

Die Tangentengleichung bestimmt man über eine Stelle x = s

t(x) = f'(s) * (x - s) + f(s) = e^s * (x - s) + e^s = x·e^s - s·e^s + e^s = e^s·x + e^s·(1 - s)

Hier kann ich für s jetzt 1 oder -1 einseten

t1(x) = e^1·x + e^1·(1 - 1) = e·x

t2(x) = e^{-1}·x + e^{-1}·(1 - (-1)) = x/e + 2/e

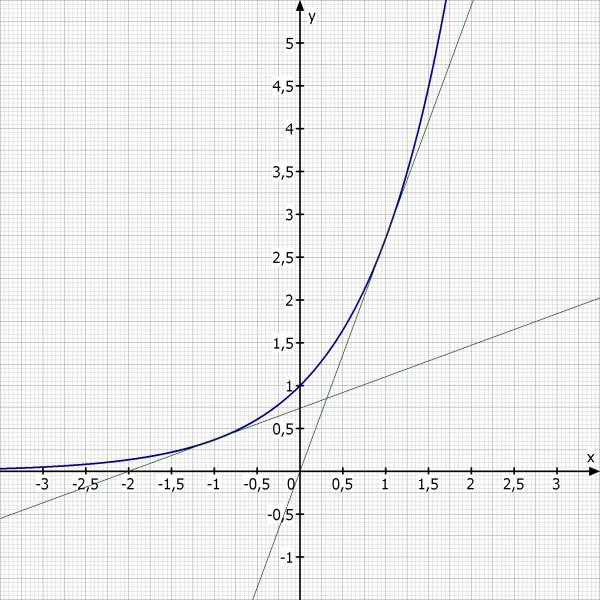
Skizze:

Comments

Schnittpunkte der Tangente mit der x-Achse sollte klar sein. Einfach t1(x) oder t2(x) = 0 setzen.

---

Danach x einsetzen und nach y ausrechnen ?

---

Wenn du das machst bekommst du für y Null heraus. Also die Nullstellen. Daher brauchst du nicht mehr einsetzen um y zu bestimmen.
Laut Zeichnung sind die Nullstellen bei -2 und 0. Das zu zeigen dürfte nicht all zu schwer sein.