Kann einer die Variable k bestimmen? E'(5)= 14,5*e^(-2,5-5k)*(-1-k)=-1,5

Question

Aufgabe:

E'(5)= 14,5*e^(-2,5-5k)*(-1-k)=-1,5

Problem/Ansatz

Kann einer bitte k bestimmen

Comments

Wie lautet den die Originalaufgabe und wo ist die her?

---

Das ist die original Aufgabe.

---

Die Aufgabe ist nicht vollständig.
Bei a.) heißt es u.a.
Vergleiche das Ergebnis mit der oben an-
gegebenen Funktion E(t).
Bitte die Vorgängeraufgabe auch einstellen.

---

Hier ist die ganze Aufgabe

Answer 1

Zur Kontrolle
k = -0.9911
und
k = -0.0583

Mach bitte die Probe.

Comments

Ich danke Ihnen, können sie mir (wenn es geht) den Rechenweg erklären/schrieben.

---

Die Werte wurden über das Newton-Verfahren
ermittelt.
Kennst du das / ist euch das schon beigebracht
worden ?
Ist die Aufgabe eine Hausaufgabe ?

Bin gern weiter behilflich.

---

Ja, haben wir schon mal gemacht, aber nur Nullstellen zu berechnen. So welche Aufgaben kommen in Prüfung vor.

---

Dann bring die Gleichung in die Nullform!

... = 0

---

14,5*e^(-2,5-5k)*(-1-k)=-1,5
der Term wird zu null umgeschrieben
14,5*e^(-2,5-5k)*(-1-k) + 1,5 = 0
weil üblich : k durch x ersetzt
f ( x ) = 14,5 * e^(-2,5-5*x) * (-1-x) + 1,5 = 0
und jetzt wird über das Newton-Verfahren
die Nullstelle(n) berechnet.

Zur Arbeitserleichterung empfiehlt es sich den
Graph plotten zu lassen

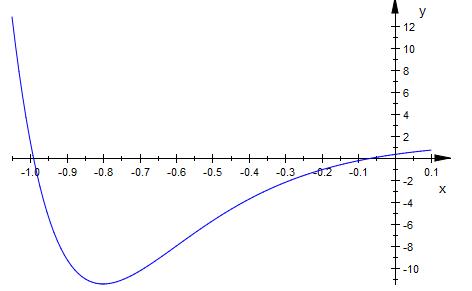
Die Berechnung " zu Fuß " dürfte relativ
arbeitsaufwendig sein

---

Du hast die Formel falsch angegeben
t = 5
Ek(5) = 14,5 * e^(-2,5-k*5) = -1,5
e^(-2,5-k*5) = -1,5 / 14.5 | ln
-2.5-5k = ln (-1,5 / 14.5 )

Geht nicht. ln aus einer negativen Zahl.

---

Muss ich nicht die erste Ableitung bilden.

---

Deine allererste Ableitung ist ok.
Es bleibt bei der Verwendug des Newton-
Verfahrens zur Lösung.
Meine ersten Ergebnisse stimmen.

Answer 2

Man kann nicht nach k umstellen. Verwende ein Näherungsverfahren (Newton)

Answer 3

......................

Kann gelöscht werden.