Was hast du denn als Ergebnis erhalten?
Vielleicht BC = 11,77 cm ?
Dann hast du fast alles richtig gemacht - nur nicht bedacht, dass eine positive Zahl zwei Quadratwurzeln hat, nämlich eine positive und eine negative.
An einer der Stelle der Berechnung muss man eine solche Wurzel ziehen und wenn man dort mit der positiven Wurzel rechnet, dann erhält man BC = 11,77 cm, rechnet man dort hingegen mit der negativen Wurzel, dann erhält man BC = 5,6 cm.
Das Trapez ist durch die Angaben also nicht eindeutig beschrieben.
Ich zeige dir mal meinen Rechenweg.
Zunächst eine annähernd maßstabsgerechte Skizze, auf der du die beiden Möglichkeiten für die Strecke CD = 8 cm schon erkennst (rot):
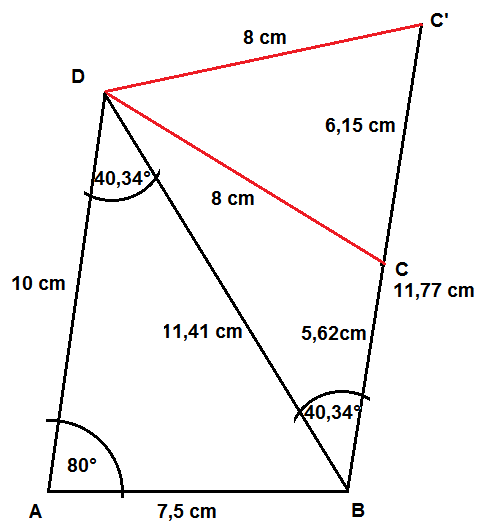
Ich benutze mehrfach den Kosinussatz. Zunächst zur Berechnung der Länge der Diagonalen BD:
f ² = AB ² + AD ² - 2 AB AD cos ( 80° )
= 7,5 ² + 10 ² - 2 * 7,5 * 10 * cos ( 80° ) = 130,2
=> f = √ 130,2 = 11,41 cm
Wiederum mit Hilfe des Kosinussatzes kann ich nun den Winkel ADB berechnen (das Zeichen "∠" bedeutet Winkel):
AB ² = AD ² + BD ² - 2 AD BD cos ( ∠ ADB )
Auflösen nach ∠ ADB:
<=> cos ( ∠ ADB ) = ( AB ² - AD ² - BD ² ) / ( - 2 AD BD )
<=> ∠ ADB = arccos ( ( AB ² - AD ² - BD ² ) / ( - 2 AD BD ) )
= arccos ( ( 7,5 ² - 10 ² - 11,41 ² ) / ( - 2 * 10 * 11,41 ) )
= 40,34 °
Da die Seiten BC und AD parallel sein sollen, ist der Winkel DBC ein Wechselwinkel zum Winkel ADB und ist damit ebenso groß wie jener.
Nun wird's leider etwas unübersichtlich, denn die Berechnung der Seite BC, wiederum mit Hilfe des Kosinussatzes führt auf eine quadratische Gleichung, in der auch noch als Faktor ein cos enthalten ist. Es gilt nach dem Kosinussatz:
CD ² = BC ² + BD ² - 2 * BC * BD * cos ( ∠ DBC )
Auflösen nach BC:
<=> BC ² - 2 * BC * BD * cos ( ∠ DBC ) = CD ² - BD ²
Das ist eine quadratische Gleichung für BC, die nun mit Hilfe der quadratischen Ergänzung nach BC aufgelöst werden muss. Die quadratische Ergänzung ergibt sich als das Quadrat der Hälfte des linearen Gliedes. Das lineare Glied ist hier der Ausdruck 2 * BD * cos ( ∠ DBC ), dessen Hälfte ist BD * cos ( ∠ DBC ) und somit ist die quadratische Ergänzung: ( BD * cos ( ∠ DBC ) ) ². Diese muss nun auf beiden Seiten der Gleichung addiert werden:
<=> BC ² - 2 * BC * BD * cos ( ∠ DBC ) + ( BD * cos ( ∠ DBC ) ) ² = CD ² - BD ² + ( BD * cos ( ∠ DBC ) ) ²
Die linke Seite kann nun mit Hilfe der zweiten binomischen Formel als Quadrat geschrieben werden:
<=> ( BC - BD * cos ( ∠ DBC ) ) ² = CD ² - BD ² + ( BD * cos ( ∠ DBC ) ) ²
Nun muss die Wurzel gezogen werden:
<=> BC - BD * cos ( ∠ DBC ) = +/- √ ( CD ² - BD ² + ( BD * cos ( ∠ DBC ) ) ² )
Schließlich kann BC freigestellt werden:
<=> BC = +/- √ ( CD ² - BD ² + ( BD * cos ( ∠ DBC ) ) ² ) + BD * cos ( ∠ DBC )
Nun ist es an der Zeit, Werte einzusetzen:
BC = +/- √ ( 8 ² - 11,41 ² + ( 11,41 * cos ( 40,34° ) ) ² ) + 11,41 * cos ( 40,34° )
= +/- √ ( 9,44782 ) + 8,6969
Und daraus ergeben sich nun die beiden Lösungen:
BC = + √ ( 9,44782 ) + 8,6969 = 11,77 cm
bzw.
BC = - √ ( 9,44782 ) + 8,6969 = 5,62 cm
Es gibt also wie bereits gesagt, zwei Lösungen, die die Vorgaben der Aufgabenstellung erfüllen.