ja - da ist ja die Aufgabestellung!
Die Punkte A (0/5/0), B(7,5/0/0), C und D (10/20/0) beschreiben die Eckpunkte eines Volleyballfeldes mit der Breite AB und der Länge AD.
Die Höhe des Netzes ist 2,4m.
Das ganze im Massstab 1:2
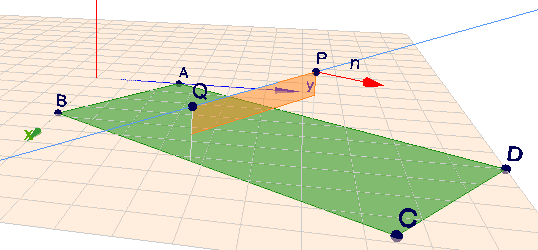
Der Punkt \(C\) ist dann $$C = B + D - A = \begin{pmatrix} 7,5 + 10 - 0 \\ 0 + 20 - 5 \\ 0 \end{pmatrix} = \begin{pmatrix} 17,5 \\ 15\\ 0 \end{pmatrix} $$Unter der Annahme, dass das Netz genauso breit ist, wie das Spielfeld, liegen die Koordinaten der oberen Eckpunkte \(P\) und \(Q\) des Netzes genau oberhalb der Mitten der Strecken \(|AD|\) bzw. \(BC\) in 2,4m Höhe. Mit $$\vec{h}=\begin{pmatrix}0\\0\\2,4\end{pmatrix}$$ wird $$P = \frac 12 (A+D) + \vec{h}=\begin{pmatrix} 5 \\ 12,5 \\ 2,4 \end{pmatrix} \\ Q = \frac 12 (B + C) + \vec{h} =\begin{pmatrix} 12,5 \\ 7,5 \\ 2,4 \end{pmatrix} \\ $$da alles schön rechtwinklig ist, ist \(\vec{AD}\) der Normalenvektor \(\vec{n}\) der Netzebene. Also $$\vec{n} = D-A= \begin{pmatrix} 10\\ 15\\ 0\end{pmatrix}$$Skalar multipliziert mit einem Punkt der Ebene (z.B. \(P\)) gibt dann die vollständige Normalform der Netz-Ebene \(E\)$$E: \space \vec{n} \vec{x} = \vec{n} \vec{P} \\ E: \begin{pmatrix} 10\\ 15\\ 0\end{pmatrix} \vec{x} = 10 \cdot 5 + 15 \cdot 12,5 + 0 \cdot 2,4 = 237,5$$man kann die Gleichung noch mit \(2/5\) multiplizieren, dann sieht es etwas gefälliger aus:$$E: \space \begin{pmatrix} 4 \\ 6 \\ 0 \end{pmatrix} \vec{x} = 95$$Die Gerade \(g\), die durch die Netzoberkante - also die Punkte \(P\) und \(Q\) verläuft, ist dann:$$g: \space \vec{x} = P + t (Q - P) = \begin{pmatrix} 5 \\ 12,5 \\ 2,4 \end{pmatrix} + t \begin{pmatrix} 7,5 \\ -5 \\ 0 \end{pmatrix}$$Gruß Werner