Vektoren: Normalform der Netz-Ebene?

Question

Aufgabe:

1.Bestimmen Sie eine Normalform der Netz-Ebene.

2.Bestimmen Sie eine Gerade, welche den Verlauf der oberen Netzkante beschreibt.

Aufgabenstellung mit Skizze im Kommentar zur Antwort von mathef

Problem/Ansatz:

1.Durch das Auflösen eines Gleichungssystems erhält man die Normalform. Ich habe da irgendwie einen Denkfehler. Kreuzprodukte hatten wir nicht, aber irgendwie kriege ich es mit dem anderen Verfahren nicht hin.

2. Habe ich es so verstanden, dass ich zwei Punkte der oberen Netzkannte bestimmen muss und dann aus diesen beiden Punkten eine Geradengleichung aufstellen soll. Klappt bei mir irgendwie auch nicht.

Ich habe irgendwie eine Denkblockade drinnen. Könnte mir jemand die freundlicherweise lösen?

Sorry, dass die Funktion oben so komisch aussieht, aber Mathpix funktioniert grad nicht bei mir.

Comments

Wie lautet denn die Originalaufgabe?

---

2.Bestimmen Sie eine Gerade, welche den Verlauf der oberen Netzkante beschreibt.

Hier kannst du vermutlich einfach den zweiten Richtungsvektor weglassen.

Wenn das Netz nicht unendlich gross ist, musst du mü und lambda einschränken.

Die z-Koordinate des Stützvektors zeigt dir vielleicht die Höhe über Boden an. Das würde aber hier heissen, dass das Netz bündig zum Boden gespannt ist.

---

Hm, eine (Kante)  Gerade, sagen wir in der „Höhe“ 2, würde

Enetz(μ,1/6)

bedeuten?

---

2.Bestimmen Sie eine Gerade, welche den Verlauf der oberen Netzkante beschreibt.

"Hier kannst du vermutlich einfach den zweiten Richtungsvektor weglassen."

Wenn du die Netzhöhe 2 haben möchtest. Stützvektor (5 | 12.5 | 2) wählen und immer noch zweiten Richtungsvektor weglassen. Weiter spekuliere ich nicht, ohne die exakte vollständige Frage zu kennen. 

---

Die Höhe des Netztes ist 2,4m. Mehr Informationen gibt es nicht.

Es ist lediglich die Funktion beschrieben und dann die Aufgaben.

Ich finds selber bisschen komisch formuliert.

---

Stützvektor (5 | 12.5 | 2,4) wählen

Rest bleibt gleich, wie ich geschrieben habe im ersten Kommentar.

---

Vorausgesetzt die Koordinatenangaben sind in Meter angegeben.

Eine vollständige Aufgabenstellung wäre immer hilfreich. Dann hat ein rumgeraten ein Ende.

Answer 1

 ja - da ist ja die Aufgabestellung!

Die Punkte A (0/5/0), B(7,5/0/0), C und D (10/20/0) beschreiben die Eckpunkte eines Volleyballfeldes mit der Breite AB und der Länge AD.
Die Höhe des Netzes ist 2,4m.

Das ganze im Massstab 1:2

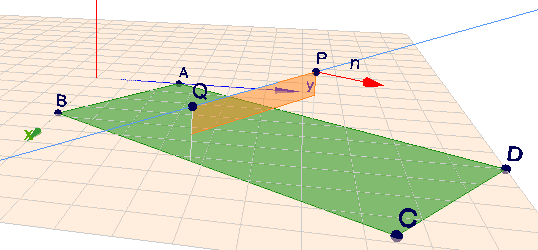
Der Punkt $C$ ist dann $$C = B + D - A = \begin{pmatrix} 7,5 + 10 - 0 \\ 0 + 20 - 5 \\ 0 \end{pmatrix} = \begin{pmatrix} 17,5 \\ 15\\ 0 \end{pmatrix}$$Unter der Annahme, dass das Netz genauso breit ist, wie das Spielfeld, liegen die Koordinaten der oberen Eckpunkte $P$ und $Q$ des Netzes genau oberhalb der Mitten der Strecken $|AD|$ bzw. $BC$ in 2,4m Höhe. Mit $$\vec{h}=\begin{pmatrix}0\\0\\2,4\end{pmatrix}$$ wird $$P = \frac 12 (A+D) + \vec{h}=\begin{pmatrix} 5 \\ 12,5 \\ 2,4 \end{pmatrix} \\ Q = \frac 12 (B + C) + \vec{h} =\begin{pmatrix} 12,5 \\ 7,5 \\ 2,4 \end{pmatrix} \\$$da alles schön rechtwinklig ist, ist $\vec{AD}$ der Normalenvektor $\vec{n}$ der Netzebene. Also $$\vec{n} = D-A= \begin{pmatrix} 10\\ 15\\ 0\end{pmatrix}$$Skalar multipliziert mit einem Punkt der Ebene (z.B. $P$) gibt dann die vollständige Normalform der Netz-Ebene $E$$$E: \space \vec{n} \vec{x} = \vec{n} \vec{P} \\ E: \begin{pmatrix} 10\\ 15\\ 0\end{pmatrix} \vec{x} = 10 \cdot 5 + 15 \cdot 12,5 + 0 \cdot 2,4 = 237,5$$man kann die Gleichung noch mit $2/5$ multiplizieren, dann sieht es etwas gefälliger aus:$$E: \space \begin{pmatrix} 4 \\ 6 \\ 0 \end{pmatrix} \vec{x} = 95$$Die Gerade $g$, die durch die Netzoberkante - also die Punkte $P$ und $Q$ verläuft, ist dann:$$g: \space \vec{x} = P + t (Q - P) = \begin{pmatrix} 5 \\ 12,5 \\ 2,4 \end{pmatrix} + t \begin{pmatrix} 7,5 \\ -5 \\ 0 \end{pmatrix}$$Gruß Werner

Comments

Vielen Dank!

Ohje, ich glaub mir fehlt das räumliche Denken.

Und wie würde man es machen, wenn die Flugbahn eines Aufschlags sich mit der Geraden G beschreiben lässt:

g: x = (5   )+  s  (-5)           (seR)

        ( 1     )       (-25)

      (   2,8   )       (2)

Man soll prüfen ob der Ball ins Netz geht

---

Stimmen die Zahlen? Der Volleyballspieler wäre ja (inklusive Armlänge) 2,8 m gross.

Wenn s grösser als 0 sein soll, wird die Flugbahn (solange gerade) gar nicht unter 2,8m kommen.

---

... wenn die Flugbahn eines Aufschlags sich mit der Geraden G beschreiben lässt:
$$g:\space x = \begin{pmatrix} 5\\ 1\\ 2,8\end{pmatrix} + s\begin{pmatrix} -5\\ -25\\ 2\end{pmatrix} \quad s \in \mathbb{R}$$Man soll prüfen ob der Ball ins Netz geht.

Ja - der geht in's Netz

.

---

Ja - der geht in's Netz

und s ist kleiner als 0, damit der überhaupt Richtung Netz geschossen wird.

Answer 2

Du hast doch 3 Gleichungen:

x1=5 + 15λ     ==>  λ = x1/15 - 1/3

x2=12,5-10λ

x3 =          12μ

Das μ kommt in den beiden ersten nicht vor, hat

also nix zu sagen.

Die erste auflösen und bei der 2. einsetzen gibt

x2=12,5-10(x1/15 - 1/3)

<=> x2=12,5-2x1/3  + 10/3

<=> 3x2 = 37,5 - 2x1 + 10

<=> 2x1 + 3x2 = 47,5

oder wenn du dasa x3 mit dabei haben willst

         2x1 + 3x2 + 0x3 = 47,5

also ist

2
3
0

ein Normalenvektor.

Comments

Ich hatte es immer mithilfe des Skalarprodukts angewendet, aber hatte es nicht geschafft die 1. aufzulösen

1.(15x1-10x2)=0

2. 12x3 = 0

Das war falsch oder?Weil man sonst nicht "reihe" für "reihe" die Gleichung bildet?

Und könntest du mir mal ein Beispiel für die zweite Aufgabe geben?

---

1.(15x1-10x2)=0

2. 12x3 = 0

Das war falsch oder?   Nein, war doch prima

Es folgt aus der ersten   x2= 1,5x1  und aus der zweiten x3=0

also sind alle Normalenvektoren von der Art

x1
1,5x1
0

also z.B.

2
3
0

zu b) Wie ist denn "Netz" definiert  und was soll die obere Kante

sein?  Eine Ebene ist doch sonst unbegrenzt .

---

Ah, vielen Dank. Jetzt habe ich es verstanden.

zu b)

Die Punkte A (0/5/0), B(7,5/0/0), C und D (10/20/0) beschreiben die Eckpunkte eines Volleyallfeldes mit der Breite AB und der Länge AD.

Die Höhe des Netztes ist 2,4m.

Achja, die Koordinaten sind alle in M angegeben.

Hier ist eine kleine Skizze. Ich hoffe mal man erkennt, etwas meine Fähigkeiten sind naja nicht sooo die besten. Alle Zahlen sind in m.