Aufgabe:
Aufgabenstellung
Eine Funktion f ist gegeben durch die Funktionsgleichung f(x)=x^3-3x
a) (1) Begründen Sie, dass der Graph von f punktsymmetrisch zum Ursprung ist.
2)Der Graph von f schließt mit der x-Achse im zweiten Quadranten die Fläche A ein.
Bestimmen Sie rechnerisch die Größe dieser Fläche.
[Zur Kontrolle: A 2,25 FE]
(
(3) Gegeben ist die Gerade g mit der Funktionsgleichung g(x)=2x, xE IR
Bestimmen Sie das Verhältnis, in dem die Gerade g die Fläche A aus (2) teilt
Problem/Ansatz:
Ich habe bei (1) auf Grund des ungeraden Exponenten und rechnerisch. Nur rechnerisch klappt es bei mir nicht?! Wo liegt der Fehler?
Wie geht (3)?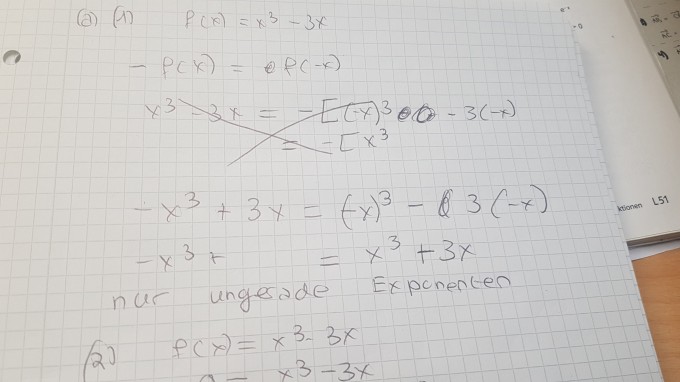
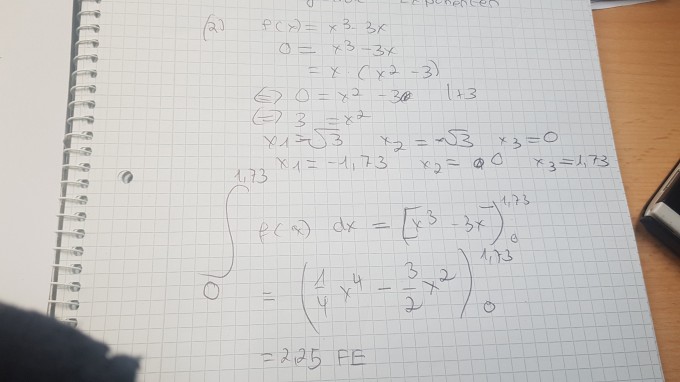 8
8