Berechnen Sie den geringsten Abstand zweier windschiefer Geraden

Question

Die beiden Geraden sehen so aus

1) g-> \( \begin{pmatrix} 1\\1\\-1 \end{pmatrix} \) + x * \( \begin{pmatrix} 2\\-1\\3 \end{pmatrix} \)

2) h-> \( \begin{pmatrix} 3\\-2\\1 \end{pmatrix} \) + y* \( \begin{pmatrix} 1\\3\\-4 \end{pmatrix} \)

Aufgabe: Ermitteln Sie den Kürzesten Abstand der zwei zueinander windschiefen Geraden
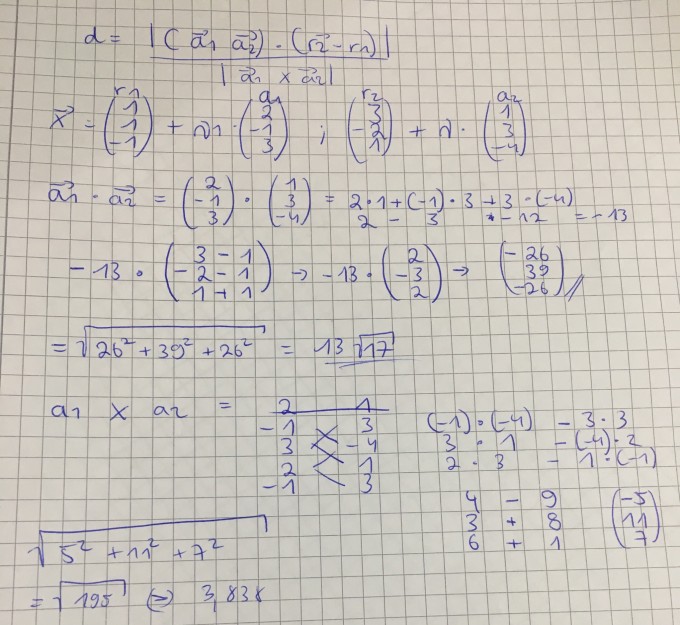 Auf einem Schmierzettel habe ich folgendes berechnet. Mein Ergebnis wäre 3,838 ist dies so richtig? 

Answer 1

Der Abstand beträgt d:=((-29)) / sqrt(195)=-2.08

Das Standardverfahren macht aus einem Orstvktor und den beiden Richtungsvektoren eine Hesse'sche Ebenengleichung, wo man den anderen Orstvektor einsetzt.

d= (r1 x r2)/sqrt((r1 x r2)^2) (O2-O1)

Dein Weg erschließt sich mir nicht auf den ersten Blick - wie gehst Du vor?

Comments

Also wir haben die Formel in der Vorlesung gegeben bekommen

Nach reinem ausrechnen und einsetzten kam ich auf das Ergebnis

---

Ach, jetzt seh ich die Formel - das sollte die sein, die ich auch angegeben habe.

und es muss a1 x a2 heissen (Vektorprodukt, wie auch im Nenner) und nicht a1 a2 (Skalarprodukt)...

---

Ja habe es in der Mitschrift gesehen dass der Prof das Rechenzeichen vergessen hat. Danke dir!

---

Wenn Du für O2 einen allgemeinen Vektor (x,y,z) einsetzt, dann hast Du eine Ebenengleichung in Hesse Normalform durch O1.

---

Habe es jetzt raus. Nochmals vielen Dank