Eine massive Hofeingangstür hat die Form eines Rechtecks mit einem aufgesetzten Parabelbogen

Question

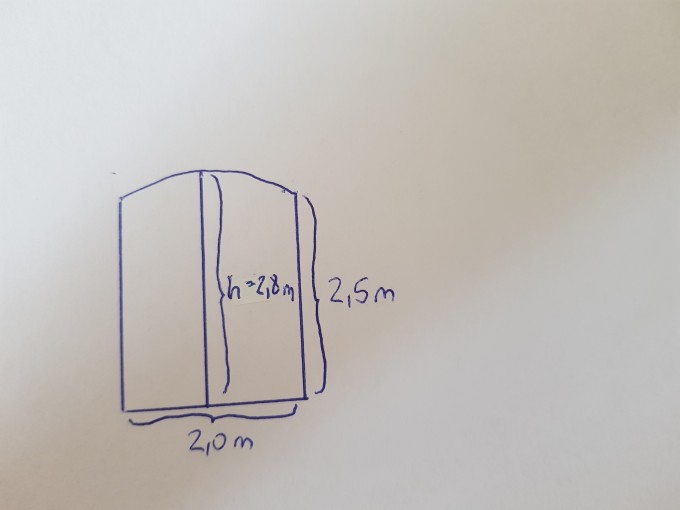
Aufgabe:

… Erstellen Sie die Gleichung für die Parabel.

Die Tür ist aus 8 cm dickem Holz gefertigt. Die Dichte beträgt 0,86 g/cm^3.

Problem/Ansatz:

Es soll f(x) = -0,3 * x^2 + 2,8 rauskommen.

Mein Problem ist, dass ich nicht auf die -0,3 komme. Von wo die 2,8 und x^2 kommen ist verständlich, aber die -0,3 sehr unverständlich für mich. Ich habe eine Skizze dazugezeichnet, um rechtlich im grünem Bereich zu sein.

Ich bedanke mich im Veraus!

Lg

Morelearning

Answer 1

Man könnte bei so einer Aufgabe verschieden herangehen, um eine Lösung zu erhalten. Der einfachste Weg ist wohl, h als Symmetrieachse aufzufassen (d.h. f(0)=2,8), denn so wird die Formel ,,schöner". Hat man dann diese Formel, dann kann man immernoch eine Verschiebung in x-Richtung einbauen.

Edit: Wie lautet deine bisherige Rechnung?

Comments

Wenn ich für x Null einsetze kommt da nicht automatisch 0 heraus? Es ist ja a * x^2. Es könnte sein, dass ich einen kompletten Unsinn rede, da ich schon seit einigen Stunden an meinen Aufgaben sitze. In den vorherigen Aufgaben waren immer Punkte gegeben und ich konnte mit denen a ausrechnen und diesmal ist nur h gegeben.

---

Du hast noch eine Verschiebung in y-Richtung, sodass deine Profilkurve dadurch beschrieben wird, wenn man h als Symmetrieachse wählt:

$$ f(x)=a\cdot x^2+c$$

---

Wie rechne ich es dann genau aus? Wenn ich nur eine Gleichung und 2 Unbekannte habe? Also ich weiß wie es geht, wenn ich zwei Unbekannte und 2 Gleichungen habe.

---

Du brauchst, wie du schon sagtest, zwei Gleichungen, um das Problem zu lösen. Welche Bedingungen kennst du aus der Aufgabe?

---

Maa danke, habe es endlich geschafft! Habe die Bedingungen gesucht und eingesetzt und die Aufgabe mit einer Matrix gelöst. Aber da hätte ich noch eine Frage. Wieso benutze ich die Funktion: a * x^2 + c und nicht die Funktion a* x^2 + b* x +c ?

---

Das kannst du auch machen, aber da h die Symmetrieachse ist (also in der y-Achse) liegt, wird b=0 sein, da eine Verschiebung in x-Richtung nicht vorliegt. Man hätte aber auch die linke oder rechte Seite der Tür nehmen können, sodass man dann tatsächlich den Ansatz $$ f(x)=a\cdot x^2+b\cdot x+c $$ nehmen muss, da eine Verschiebung in x-Richtung vorliegt.

---

Habe mir das nochmal angeschaut, weil mit deiner Erklärung und habe gesehen, dass ich einen Tippfehler in der Matrix hatte und deswegen ist bei b nicht 0 rausgekommen sondern eine 2. Hatte mich deswegen gewundert, wieso b nicht in der Funktion einberechnet wird. Danke nochmals. Ich verstehe wegen deinen ganzen Tipps das ganze Thema besser. Ich weiß es zu schätzen, dass du es mir nicht einfach vorgerechnet hast! Ich hätte sonst nicht wirklich mitgelernt glaub ich. Danke nochmals und tut mir leid, für die Umstände die du dir gemacht hast, weil ich manchmal zu blond bin. (Nichts gegen Blonde)

---

Freut mich, dass du das Problem selbst rechnerisch lösen konntest. :)

---

Habe mir gerade meine vorherige Antwort durchgelesen und bemerkt, dass ich garkeinen Sinn ergebe. Normalerweise ist mein Deutsch auf einem höherem Niveau, tut mir leid, dass du dir das Durchlesen musstest :D

---

Habe noch eine Frage dazu:

Wenn ich f(x)= a * x² + b * x + C verwenden möchte nehme ich die Punkte

z.B: Q (-1/0)

       R (1/0)

       S ?

Habe für S (0/2,8) probiert und S (1/2,5), aber immer das falsche Ergebnis bekommen.

Ergebnis soll f(x) = 2,8 - 0,3 * x²  sein.

Bitte um Hilfe!

---

Hallo Pattis,

Q hat die Koordinaten (-1|2,5), denn die Parabel geht nicht bis zum Fußboden, sondern liegt auf der oben Kante des rechteckigen Schrankteils.

---

Vielen Dank für die Hilfe!