Welche der folgenden Mengen sind Untervektorräume? U5:= { (x,y) € R^2 | x^2 + y^6 = 0 }

Question

Aufgabe:

Welche der folgenden Mengen sind Untervektorräume? U5:= { (x,y) € R^2 | x^2 + y^6 = 0 }

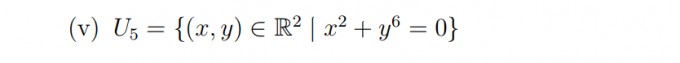
Problem/Ansatz:

Ich weiß nicht ganz genau wie ich das hier zeigen soll.

Der Nullvektor ist ja offensichtlich in U5. 
nun muss ich noch die Abgeschlossenheit bzgl. "+" und "*" zeigen.
Mein Ansatz war:

sei v = (a,b) und v' = (a',b')  dann ist (x,y) = (a+a', b+b')

also muss ich hier zeigen (a+a')^2 + (b+b')^6 = 0
Jetzt weiß ich leider nicht mehr weiter bzw. ich bin mir nicht einmal sicher ob ich genau das zeigen soll.

Comments

Tipp: Die Anzahl der Elemente von U₅ ist sehr überschaubar.

---

Vielen dank für die schnelle Hilfe.
leider kann ich mit diesem Tipp nicht viel anfangen.
Wieso ist denn die Anzahl der Elemente von U₅ sehr überschaubar?

damit x^2 + y^6 = 0 sein kann, muss y = -x^2 sein oder x = -y^6.
und das gilt doch für alle x,y in ℝ.

---

Oder ist es mir möglich für y^6 = -x^2 einzusetzten.
damit hätte ich dann (a+a')^2 -(a+a')^2 = 0.
und das wäre dann ja 0 = 0

---

U₅ enthält wie du bereits erwähnst den Nullvektor. Sonst gilt immer x² + y⁶ > 0, d.h. U₅ enthält keine weiteren Elemente.

---

ah ok jetzt hab ich es vielen dank!

Answer 1

Du musst es eigentlich nur für den Nullvektor zeigen.

Den x^2 und x^6 sind beide immer positive Zahlen.

=> x^2 + x^6 ergibt genau dann 0, wenn x = 0 und y = 0.

Answer 2

Hallo

gerade Potenzen von reellen Variablen sind immer >=0 , damit hast du direkt dein Mini U

Gruß lul