Jordan Normalform und Minimalpolynom einer Matrix

Question

Aufgabe:

Gegeben sei die Matrix

\( \begin{pmatrix} 0 & 0 & 0 & b_1 \\ 0 & 0& 0 & b_2 \\ 0 & 0 & 0 & b_3 \\ a_1 & a_2 & a_3 & 0 \end{pmatrix} \)

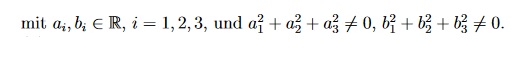
a) besitzt A eine Jordansche Normalform als Matrix aus M(4,ℝ)?

b) Zeigen Sie, dass das Minimalpolynom von A durch μ_A=x(x²-c) mit c=a₁b₁+a₂b₂+a₃b₃ gegeben ist.

Problem/Ansatz:

Ich sitz an der Aufgabe nun leider schon mehrere Stunden und komm leider absolut nicht drauf. Kann mir das jemand mal Stück für Stück vormachen und eventuell auch erklären? 

Wäre sehr dankbar über Hilfe.