 Aufgabe:
Aufgabe:
HOSENTASCHE
Gegeben ist die Funktionsschar f{a}(x)=(ax+1)*e^-ax ; xER ; aER.
Die Graphen dieser Funktionsschar f{a} sind G{a}.
a) Ernitteln Sie die Nullstellen von f{a} in Abhängigkeit von a. Bestimmen Sie den Wert des Parameters a, für den die Scharfunktion keine Nullstelle hat, und geben Sie die zugehörige Funktionsgleichung an.
b) Geben Sie das Verhalten der Funktionswerte von f{a} für x -> unendlich & x -> -unendlich in Abhängigkeit von a (a ungleich 0) an.
c) Weisen Sie nach, dass alle Graphen G{a} (a ungleich 0) den lokalen Extrempunkt E (0|1) haben. Ohne Herleitung dürfen Sie verwenden: f‘‘{a}(x)=e^-ax ((a^3)x-a^2). Alle Wendepunkte der Graphen G{a} (a ungleich 0) liegen auf einem parallel zur x-Achse verlaufenden Graphen einer Funktion g. Geben Sie die Funktionsgleichung von g an. Auf die Untersuchung der hinreichenden Bedingung kann verzichtet werden.
d) Zeigen Sie, dass F{a}(x)=(-x-(2/a))*e^-ax ;xER ; aER ;a ungleich 0 eine Stammfunktion von f{a} ist.
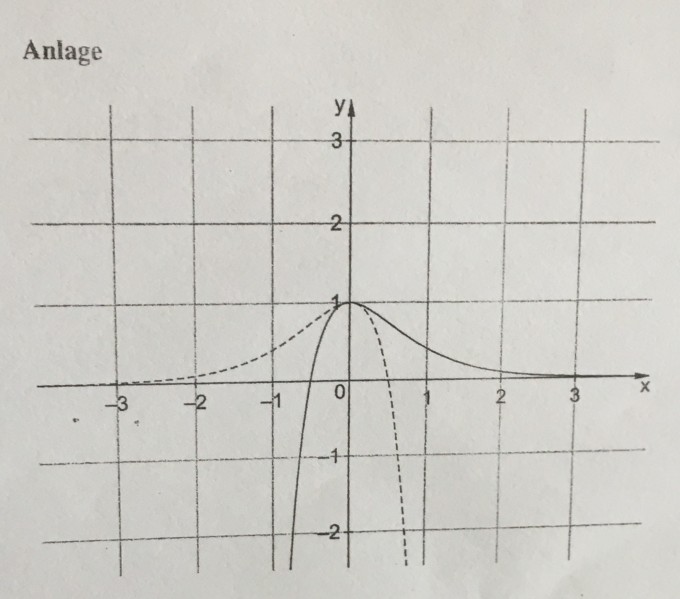
e) In der Anlage sind zwei Graphen der Funktionsschar f{a} dargestellt. Begründen Sie, dass es sich dabei um die Graphen G2 und G_2 handelt und beschriften Sie die Graphen in der Anlage.
Eine Bekleidungsfirma möchte Gesäßtaschen von Jeans wie abgebildet besticken. Zur Modellierung des Motivs werden die Graphen G2 und G_2 genutzt (vgl. Anlage).
Der untere Rand des Motivs soll ebenfalls durch 2 Graphen dargestellt werden, so dass die x- bzw.y- Achse Symmetrieachsen des Motivs sind.
Geben Sie jeweils eine Funktionsgleichung an und zeichnen Sie die Graphen möglichst vollständig in der Anlage.
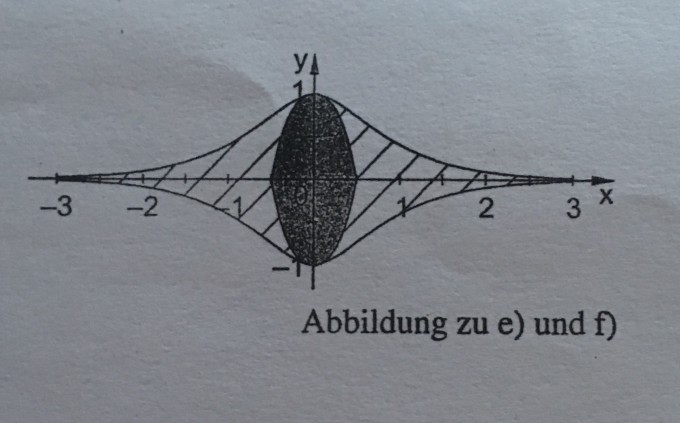
Der in der Abbildung schraffiert dargestellte Teil des Motivs soll bestickt werden. Berechnen Sie die Größe dieser Fläche im Intervall [-3 ; 3].
f) Der Teil der in der Abb. grau gefärbten Fläche, der oberhalb der x-Achse liegt, soll nun durch den Graphen einer quadratischen Funktion p mit der Gleichung p(x)=-bx^2+c (b,cER) so dargestellt werden, dass die Größe dieser Teilfläche unverändert (e-2) FE beträgt. Der lokale Extrempunkt bleibt der Punkt E(0|1).
Ermitteln Sie den Wert für c und stellen Sie eine Gleichung auf, aus der b berechnet werden kann.
Problem/Ansatz:
Ich bin eigentlich eine relativ gute Schülerin in Mathe, jedoch auch nach mehrmaligen durchgehen, stehe ich mit dieser Aufgabe vor einer Wand und wäre für jede Hilfe sehr dankbar!