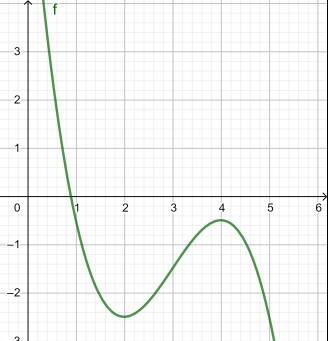
Die Abbildung zeigt den Graphen der Funktion f mit f(x)= -0,5 mal x hoch 3 + 4,5 mal x hoch 2 - 12 mal x + 7,5 (x element R)
1.Begründen Sie ohne Rechnung,dass die Gleichung 0= -0,5 mal x hoch 3 + 4,5 mal x hoch 2 - 12 mal x + 7,5
2.Berechnen Sie die Koordinaten des Wendepunktes des Graphen von f.
ich habe die Zeichnung mit Geogebra erstellt und hoffe es ist in ordnung,Ich bitte um den kompletten Lösungsweg eventuell eine kurze erklärung für das bessere verständnis wäre nett