Die Abbildung zeigt den Graphen einer ganzrationalen Funktion 4. Grades.

Question

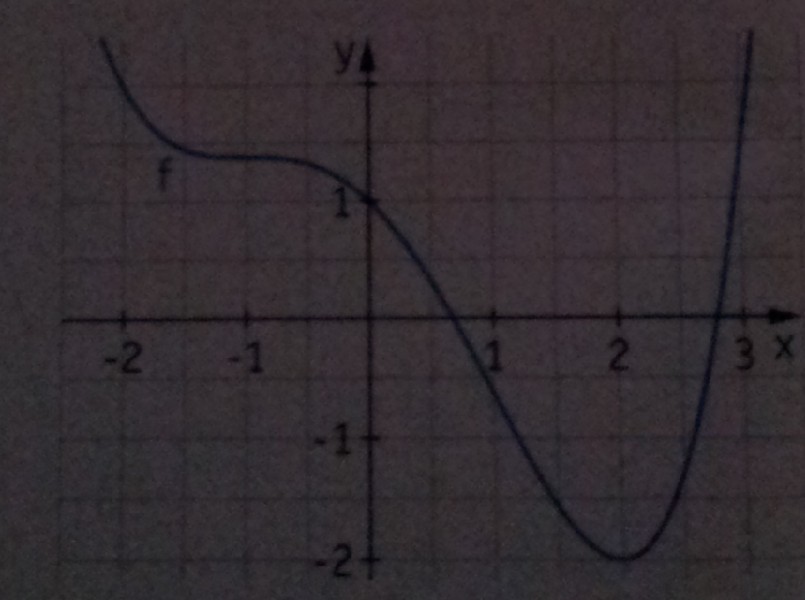
wir haben in der Schule heute eine Aufgabe bearbeitet und ich habe sie nicht richtig verstanden.

 

Uns wurde ein Graph einer ganzrationalen Funktion 4. Grades gezeigt. Wir sollten anschließend begründet sagen, ob in der Abbildung alle Punkte mit waagerechter Tangente zu sehen sind.

Mein erster Gedanke war: Da die Funktion den Grad 4 besitzt, muss die Funktion ja 4 NS haben. Mein Lehrer sagt aber das sie höchstens 4 Nullstellen hat, sie kann also auch 3 haben. Er sagte ich solle mir nochmal das Fernverhalten der Funktion anschauen.

Ich weiß jetzt aber nicht wie mir das helfen soll herauszufinden, ob die Funktion noch weitere Punkte mit waagerechter Tangente besitzt.

Answer 1

Hi,

eine waagerechte Tangente bedeutet, dass die erste Ableitung 0 sein muss.

Die erste Ableitung eines allgemeinen Polynoms 4ten Grades sieht so aus.

y=ax^4+bx^3+cx^2+dx+e

f'(x)=4ax^3+3bx^2+2cx+d


Wir haben mit der ersten Ableitung also ein Polynom dritten Grades. Das bedeutet maximal drei Nullstellen.

Wenn wir uns wieder dem Graphen zuwenden, sehen wir eine Extremstelle rechts unten -> dort haben wir die Steigung 0 und damit eine waagerechte Tangente.

Im linken oberen Quadranten haben wir allerdings einen Sattelpunkt. Das bedeutet, dass wir eine doppelte Nullstelle haben.

Damit sind alle Nullstellen für das Polynom dritten Grades aufgebraucht und wir haben keine weitere waagerechte Tangente mehr.


Grüße

Comments

Vielen Dank für die Antwort.
Also sieht man erst am Grad der Ableitung, wie viele Nullstellen der Graph hat? Verstehe ich das richtig?


LG

---

Die Anzahl der Nullstellen hat mit der Ableitung nichts zu tun ;).

Die Anzahl der (reellen) Nullstellen kann man allgemein nicht so leicht feststellen. Man kann nur eine Aussage über die maximale Anzahl machen. Bei einem Polynom dritten Grades wären das maximal 3 Nullstellen ;).

---

Sorry für die blöde Frage, aber was ist ein Polynom?

---

Ein Polynom ist eine Funktion der Gestalt

f(x)=ax^n+bx^{n-1}+...+c

Wobei die Exponenten natürlich sind.

---

Ich musste die Aufgabe auch machen und habe sie nicht ganz verstanden. Vor allem nicht warum ein sattelpunkt eine doppelte nullstelle ist, zumal ich auch nicht verstehe, was dies bedeutet.

---

Die "doppelte" Nullstelle bezieht sich auf die Ableitung.

Ich hatte gesehen, dass Du auch nen Extra Thread dafür aufgemacht hast. Ist dann alles klar? ;)