Die Frage hier ist doch: "Was ist \(\alpha\)?"
Wenn man von einem Kegel die Mantelfläche zu einem ebenen Kreissektor abrollt ..
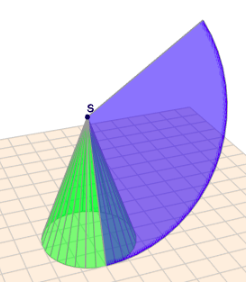
.. so wie hier auf dem Bild vom grünen Kegel die blaue Fläche abgerollt wurde, so ist \(\alpha\) der Mittelpunktswinkel des blauen Kreissektors.
Sei \(s\) die Mantellinie des Kegels, dann ist die Länge \(L\) des Kreisbogens des Kreissektors$$L = 2\pi s \frac{\alpha}{360°}$$Und \(L\) ist gleichzeitig der Umfang der Grundfläche des Kegels mit Radius \(r\)- also:$$L = 2\pi s \frac{\alpha}{360°} = 2\pi r \implies s = \frac {360°}{\alpha} r$$Nach Pythagoras ist$$h^2 = s^2 - r^2$$und somit wird aus$$V = \frac 13 \pi r^2 h = \frac 13 \pi r^2 \sqrt{s^2 - r^2} = \frac 13 \pi r^2 \sqrt{\frac{360°^2}{\alpha ^2}r^2 - r^2} = \frac 13 \pi r^3 \sqrt{\frac{360°^2}{\alpha ^2} - 1} $$