Aufgabe:Ein Abenteuer-Spielplatz soll eine möglichst große rechteckige Fläche zugewiesen bekommen. Der Spielplatz liegt im Gleisbogen eines Industriegleises.
Das Gleis quert die Hauptstraße im Punkt A und Nebenstraße im rechten Winkel im Punkt B
Zwischen den Punkten A und B kann das Gleis durch eine quadratische Funktion (Parabel) beschrieben werden.
Die Nebenstraße mündet im rechten Winkel in die Hauptstraße ein.
a) Ermitteln Sie rechnerisch die Funktion g(x) = rx^2+sx+d welche den Verlauf des Industriegleises zwischen den Punkten A und B beschreibt. Nutzen Sie hierzu die Lage der Bahnübergänge A und B und die Steigung der Funktion g(x) im Punkt B
b) Bestimmen Sie die Fläche f(a,b) eines Spielplatzes mot Breite a indem Sie die Länge b als Funktion von a ermitteln
c) Ermitteln Sie den Wert von a für den die Fläche f(a) maximal wird
d) Welche maximale Größe hat der Spielplatz?
e) Wie groß ist der Anteil der Spielplatzfläche an der durch Industriegleis, Hauptstraße und Nebenstraße begränzten Gläche?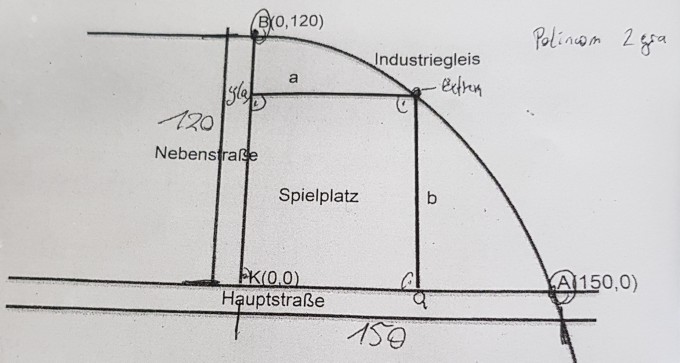
Problem/Ansatz:
Ich habe die Steigung bestimmt:
m=y1-y2÷x1-x2 =120÷-150=-0,8
Dann die gegebenen Punkte in die Gleichung g(x)=rx^2+sx+d eingesetzt:
120=r×0^2 + s×0+d
120= d
0= r×150^2+s×150+120
0= 22500r+150s+120
und ab hier komme ich nicht weiter.
Habt ihr einen Tipp, wie ich das ganze angehen soll? Was muss ich beachten und was kann ich zum lösen ähnlicher Aufgaben übernehmen?
Falls jemand von euch die Aufgabe lösen kann und den Lösungsweg grob verständlich beschreibt wäre ich sehr dankbar.