Wissensartikel "Mittelwerte"

Question

Man unterscheidet ein arithmetisches, ein harmonisches und ein geometrisches Mittel. Je nach Fragestellung und Zusammenhang werden diese eingesetzt.

Arithmetisches Mittel
Die Summe von n Zahlenwerten dividiert durch ihre Anzahl n heißt arithmetisches Mittel der n Zahlenwerte.
Beispiel: Berechnung der Durchschnittsnote einer Klassenarbeit. Gegeben ist folgende Notenverteilung:

Note	1	2	3	4	5	6
Anzahl	4	5	8	3	2	2

Dann berechnet sich die Durchschnittsnote so:
(4 ·1+5 ·2+8 ·3+3 ·4+2 ·5+2 ·6)/(4+5+8+3+2+2)=3.

Harmonisches Mittel
Werden n gleiche Maßeinheiten mit jeweils der zugehörigen Geschwindigkeit v₁, v₂, …, v_n bewältigt, dann berechnet sich die Durchschnittsgeschwindigkeit als Kehrwert des arithmetischen Mittels der Kehrwerte der Geschwindigkeiten.
Beispiel: Die ersten 100 m³ eines Schwimmbeckens werden mit einer Füllgeschwindigkeit von 20 m³ pro Stunde gefüllt, die zweiten 100 m³ wegen Einsatzes einer weiteren Pumpe mit 50 m³ pro Stunde und die dritten 100 m³ nach Einsatz einer dritten Pumpe mit einer Füllgeschwindigkeit von 200 m³ pro Stunde. Wie groß ist die durchschnittliche Füllgeschwindigkeit?
Rechnung 3/(1/20+1/50+1/200)=40. Antwort: Die durchschnittliche Füllgeschwindigkeit ist 40 m³ pro Stunde.

Geometrisches Mittel
Ändert sich ein Wachstum in n Zeiteinheiten z nacheinander mit den Wachstumsfaktoren q₁, q₂, .., q_n, so berechnet sich der durchschnittliche Wachstumsfaktor in der Zeiteinheit z als n-Wurzel aus dem Produkt der n Wachstumsfaktoren.
Beispiel:  Ein Guthaben wird in den ersten vier Jahren mit 3 Prozent, in den nächsten 3 Jahren mit 2 Prozent und dann mit 1 Prozent verzinst. Welcher über die Jahre konstante Zinssatz hätte nach 10 Jahren das gleiche Kapital ergeben?
Rechnung \( \sqrt[10]{1,03^4·1,02^3·1,01^3} \) ≈1,021. Antwort: Der durchschnittliche Jahreszinssatz nach Ablauf von 10 Jahren ist ungefähr 2,1%.
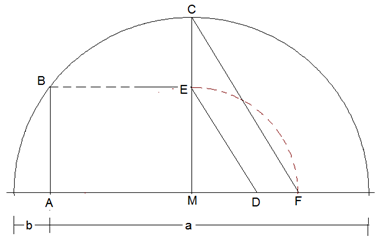
m_a, m_g und m_h seien die  drei verschiedenen Mittelwerte zweier Zahlen a und b. Dann gilt m_a= (a+b)/2,  m_g=√(a∙b) und m_h= 2/(1/a+1/b), und wie man mit etwas Termumformung und Gleichungslehre bestätigen kann: (*)  m_h/m_g =m_g/m_a .
In der untenstehenden Skizze ist teilt A den Durchmesser des Thaleskreises im Verhältnis a:b. Dann ist nach Euklid AB=ME=MF=m_g und MC=m_a  sowie nach (*) und nach einem Strahlensatz MD=m_h. Damit ist geometrisch gezeigt, dass m_h≤m_g≤m_a. Der Fall der Gleichheit gilt für a=b.