hallo
1)
f(x) = (1/2)*x^3-4*x^2+8x
nullstellen(x-achsen-schnittpunkte) finden
(1/2)*x^3-4*x^2+8x = 0
(1/2)*x(x^2-8x-16) = 0
x1 = 0.
x^2-8x-16 = 0
x2,x3 = 4 ± 0
x2,x3 = 4
wir erhalten einen schnittpunkt bei x1 = 0 und eine
doppelte nullstelle bei x2 = x3 = 4.
suche nach extrempunkten.
f'(x) = (3/2)*x^2-8x+8
(3/2)*x^2-8x+8 = 0
x^2-16/3x+16/3 = 0
x1,x2 = 16/6 ± √(16^2/36-16*12/36)
x1,x2 = 16/6 ± √(64/36)
x1,x2 = 16/6 ± 8/6)
x1 = 4
x2 = 4/3
die erste ableitung ist bei x1 = 4 und bei x2 = 4/3 gleich null.
die notwendige bedingung, dass x1 und x2 extrempunkte sind, ist erfüllt.
wenn auch die hinreichende bedingung f''(x) ≠ 0 an der stelle x1 und x2 erfüllt
ist, haben wir mit sicherheit extrempunkte bei x1 und x2
f''(x) = 3x-8
x1 einsetzen
f''(4) = 3*4 - 8 = 4 daraus folgt, dass an der stelle x1 ein extrempunkt ist.
f''(4/3) = 3*4/3 - 8 = -4 daraus folgt, dass an der stelle x2 ein extrempunkt ist.
die funktion f(x) = (1/2)*x^3-4*x^2+8x hat bei x1 = 4 und
bei x2 = 4/3 ≈ 1.33 einen extrempunkt.

2.
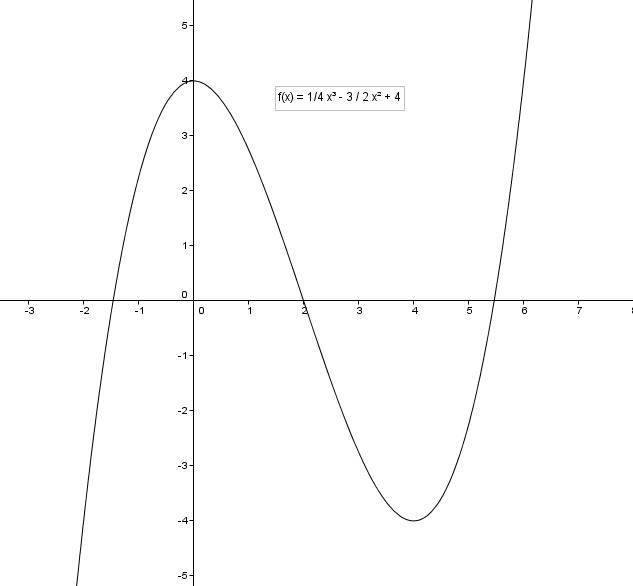
f(x) = (1/4)x^3-(3/2)x^2+4
nullstellen(schnittpunkte auf der x-achse) suchen.
x^3-6x^2+16=0
durch probieren erhalten wir eine nullstelle bei x = 2
damit können wir einen linearfaktor (x-2) abspalten.
wir berechnen das reduzierte polynom mittels polynomdivision.
x^3 - 6x^2 + 16 : x-2 = x^2 - 4x - 8
x^3 - 2x^2
—————————————
- 4x^2 + 16
- 4x^2 + 8x
—————————————
- 8x + 16
- 8x + 16
—————————————
0
glück gehabt :D, die gleichung ist ohne rest teilbar, das reduzierte polynom ist
x^2 - 4x - 8
damit können wir schreiben: x^3 - 6x^2 + 16 = (x-2)(x^2-4x-8)
bei x1 = 2 können wir sofort eine nullstelle erkennen.
wenn es noch weitere nullstellen gibt, muss x^2-4x-8 = 0 eine relle lösung liefern.
x^2-4x-8 = 0
x2, x3 = 2 ± √10
x2 = 2 + √10
x2 ≈ 5.16
x3 = 2 - √10
x3 ≈ -1.16
insgesamt haben wir also herausgefunden, dass die funktion f(x) = (1/4)x^3-(3/2)x^2+4
drei nullstellen und drei achsenschnittpunkte hat.
suche nach extrempunkten
f'(x) = 3/4 x^2 - 3x
3/4 x^2 - 3x = 0
3x( 1/4 x - 1) = 0
x1 = 0, x2 = 4
das prinzip ist dasselbe wie bei der ersten aufgabe:
die erste ableitung ist bei x1 = 0 und bei x2 = 4 gleich null.
die notwendige bedingung, dass x1 und x2 extrempunkte sind, ist erfüllt.
wenn auch die hinreichende bedingung f''(x) ≠ 0 an der stelle x1 und x2 erfüllt
ist, haben wir mit sicherheit extrempunkte bei x1 und x2
dafür müsen wir wieder die zweite ableitung berechnen.
f''(x) = 6/4 x - 3
und prüfen, ob die hinreichende bedingung erfüllt ist.
f''(0) = - 3 ≠ 0 daraus folgt, dass an der stelle x1 = 0 ein extrempunkt ist
f''(4) = 5 ≠ 0 daraus folgt, dass an der stelle x2 = 4 ein extrempunkt ist
et voilà, wir haben zwei extrempunkte gefunden.
die extrempunkte der funktion f(x) = (1/4)x^3 - (3/2)x^2 + 4
sind x1 = 0, x2 = 4
3.
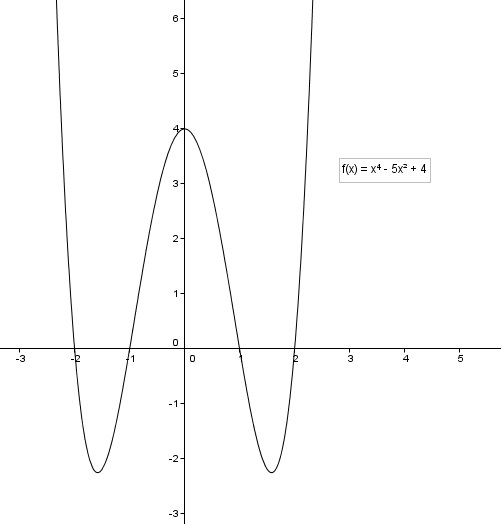
f(x) = x^4 - 5x^2 + 4
suche nach nullstellen
wir setzen x^2 = z
f(z) = z^2 - 5z + 4
z1,z2 = 5/2 ± √(25/4 - 16/4)
z1,z2 = 5/2 ± √(9/4)
z1,z2 = 5/2 ± 3/2
z1 = 4
z2 = 1
x^2 = z
x = √z
x1, x2 = ±√(z1) = ±√(4) = ±2
x3, x4 = ±√(z2) = ±√(1) = ±1
wir haben vier nullstellen gefunden:
x1 = 2
x2 = -2
x3 = 1
x4 = -1
suche nach extrempunkten
das prinzip ist dasselbe wie bei den vorigen aufgaben
f'(x) = 4x^3 - 10x
4x^3 - 10x = 0
4x(x^2-2.5) = 0
x1 = 0
x2 = √(5/2) ≈ 1,58
x3 = -√(5/2) ≈ -1,58
f''(x) = 12x^2 - 10
f''(0) ≠ 0 daraus folgt, dass an der stelle x1 ein extrempunkt ist
f''(√(5/2)) ≠ 0 daraus folgt, dass an der stelle x2 ein extrempunkt ist
f''(-√(5/2)) ≠ 0 daraus folgt, dass an der stelle x3 ein extrempunkt ist
mfg