Komplexe Zahlen einzeichnen

Question

ich wiederhole gerade ein paar Aufgaben und hab bei einer Lösung ein Verständnisproblem.

Es sollen alle Zahlen mit Re(1/z )<1 eingezeichnet werden.

$$ \frac{1}{z} = \frac{1}{x+yi}= \frac{1}{x+yi}·\frac{x-yi}{x-yi} = \frac{x-yi}{x^{2}+y^{2}}, \text{ d. h. } Re(\frac{1}{z})= \frac{x}{x^{2}+y^{2}} \rightarrow  \frac{x}{x^{2}+y^{2}} < 1 \Longleftrightarrow x<{x^{2}+y^{2}} \text{ und folgende Äquivalenz habe ich nicht verstanden: } \Longleftrightarrow (\frac{1}{2})^{2} < (x -\frac{1}{2})^{2} + y^2 $$

Answer 1

Hier der Teil den du auch schon verstanden hattest.

Re(1/z) < 1

Re(1/(x + yi)) < 1

Re((x - yi)/((x + yi)(x - yi))) < 1

Re((x - yi)/(x^2 + y^2)) < 1

Re(x/(x^2 + y^2) - yi/(x^2 + y^2)) < 1

x/(x^2 + y^2) < 1

Hier zusätzlich der Teil den du noch nicht verstanden hattest.

x/(x^2 + y^2) < 1

x < x^2 + y^2

x^2 - x + y^2 > 0

x^2 - x + 1/4 + y^2 > 1/4

(x - 1/2)^2 + y^2 > (1/2)^2

Jetzt solltest du erkennen wie ausschauen sollte oder?

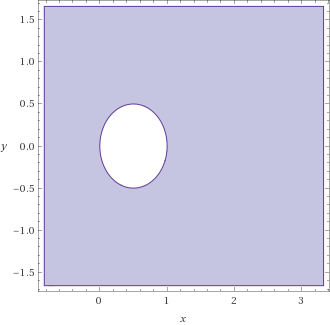
Sorry. Wolframalpha skaliert hier nicht gut.

Comments

Danke für die schnelle Hilfe :).An der quadratischen Ergänzung bin ich gescheitert

---

D.h. ich zeichne von dem Punkt (1/2|0)

Einen Kreis mit dem Radius 1/4 und alle Zahlen außerhalb von dem Kreis erfüllen die Bedingung?

Danke nochmal für deine Hilfe :)

---

Fast. Wie groß ist der Radius? Denk an die Kreisgleichung!

(x - Mx)^2 + (y - My)^2 = r^2
ist ein Kreis mit dem Mittelpunkt M(Mx | My) und dem Radius r.

---

Ach Wurzel aus 1/4 also 1/2 oder liege ich komplett falsch?

---

1/2 ist richtig. Warum habe ich oben wohl statt

(x - 1/2)^2 + y^2 > 1/4

eben

(x - 1/2)^2 + y^2 > (1/2)^2

geschrieben. Eigentlich nur damit du es etwas einfacher hast :)

---

Super Dank dir habe ich es verstanden

Answer 2

Hallo

 schreib z=x+iy, dann 1/z dann den Realteil. dannsolltest du auf x<x^2+y^2 kommen , alles auf eine Seite, quadratische Ergänzung, und du siehst es.

bei solchen Aufgaben ist es immer zu raten z=x+iy zu verwenden, weil man dann auf di bekannten formen in der x-y Eben kommt.

Gruß lul

Comments

Danke lul,

ich habs dem Mathecoach schon geschrieben, dass ich den Schritt wo die quadratische Ergänzung angewandt wurde bei meiner Musterlösung nicht verstanden habe. Doch durch eure Hilfe schon.

Danke nochmal ☆