Hallo Pete,
Ich unterstelle mal, dass Dir der Sinussatz bekannt ist. Hier angewendet bedeutet er, dass $$\frac{\sin \alpha}{|BC|} = \frac{\sin \beta}{|CA|}$$Daraus folgt dann mit den konkreten Daten$$\sin \alpha = \frac {|BC|}{|CA|} \sin \beta = \frac{8\text{cm}}{5\text{cm}} \sin 50° \approx 1,23 \gt 1$$Das Ergebnis ist größer als \(1\). Der Sinus kann aber keine Werte annehmen, deren Betrag größer als \(1\) ist. Also gibt es kein Dreieck mit diesen Werten.
Geometrisch betrachtet sieht es so aus:
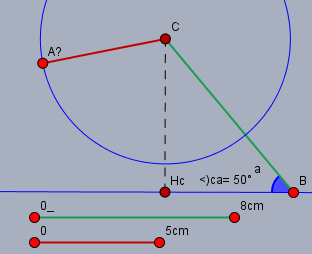
obiges Bild zeigt den Versuch einer Konstruktion. Der Punkt \(A\) müsste sowohl auf dem blauen Kreis als auch auf der blauen Geraden liegen. Diese schneiden sich aber nicht, also existiert auch der Punkt \(A\) nicht.
Anders ausgedrückt: Jede Seite in einem Dreieck muss mindestens so lang sein, wie jede Höhe mit der sie ein Ende gemeinsam hat.
Das folgt aus dem Umstand, dass in einem rechtwinkligen Dreieck jede Kathete nicht länger sein kann als die Hypotenuse. Die Seite \(|CA|\) wäre hier die Hypotenuse und die schwarz gestrichelte Strecke \(h_c\) die Kathete im (fiktiven) rechtwinkligen Dreieck \(\triangle AH_cC\) (nicht gezeichnet!).
Mit \(|BC|\) und \(\beta\) (der blaue Winkel) ist die Höhe \(h_c\) bereits gegeben:$$h_c = |BC| \cdot \sin \beta =8\text{cm} \cdot \sin 50° \approx 6,13 \text{cm} \gt 5\text{cm} = |CA|$$ und \(h_c\) ist länger als \(|CA|\). Also ist das Dreieck nicht konstruierbar.