Ein Wanderer geht in hügeligem Gelände von A nach B.
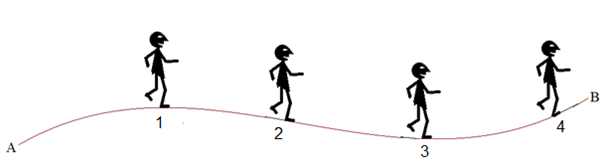
In den die Positionen 1 und 3 er geht er weder bergauf noch bergab. In der Position 2 geht er bergab und in der Position 4 geht er bergauf.
Sowohl umgangssprachlich als auch mathematisch spricht man von verschiedenen Steigungen auf den Wege des Wanderers. Eine „Steigung bergab“ heißt in der Mathematik „negative Steigung“. In den Positionen 1 und 3 spricht man mathematisch von der „Steigung 0“. Jeder Steigung wird in er Mathematik ein Zahlenwert zugeordnet. Dabei wird jede Kurve als ein Schnitt durch ein Gelände gesehen, das von links nach rechts durchwandert wird.
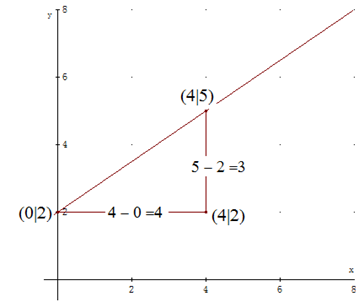
Um den Zahlenwert einer Steigung an einer Stelle der Kurve zu bestimmen, erinnern wir uns an den Zahlenwert der Steigung einer Geraden. Im Koordinatensystem haben wir diesen Wert mit Hilfe eines sogenannten Steigungsdreiecks bestimmt. Dabei wurden die Längen der zu den Koordinatenachsen parallelen Katheten des Steigungsdreiecks als Differenz zweier y-Werte bzw. als Differenz zweier x-Koordinaten berechnet und durcheinander dividiert. Auf diese Weise entsteht ein sogenannter Differenzenquotient (hier):
\( \dfrac{ \text{Differenz der y-Werte}}{\text{Differenz der x-Koordinaten}} \) =\( \dfrac{5-2}{4-0} \) =\( \dfrac{3}{4} \) .
Man sagt: „Der Differenzenquotient ist gleich der Steigung der Geraden“.
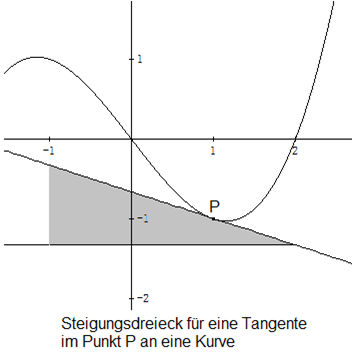
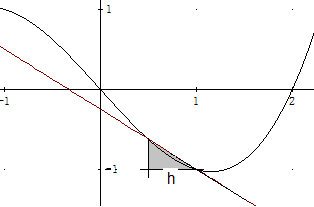
Wenn keine Geraden betrachtet werden, soll die Steigung in einem Punkt gleich der Steigung der Tangente in diesem Punkt sein. (Die Tangente an eine Kurve in einem Punkt der Kurve hat mit der Kurve in der Nähe des Punktes nur diesen Punkt gemeinsam (siehe Abbildung). Die waagerechte Kathete des Steigungsdreiecks ist hier (geschätzt) dreimal so lang, wie die senkrechte. Der Betrag der Steigung ist also 1/3 und da es im Punkt P abwärts geht, ist der geschätzte Wert der Steigung im Punkt P gleich -1/3.
Nun ist die Tangente an eine Kurve mit großer Exaktheit nicht ganz einfach zu bestimmen. Die Tangente findet man am besten über einen Näherungsprozess nach dem Prinzip: Die Tangente ist die Grenzlage der Sekante, bei der die beiden Schnittpunkte zwischen Kurve und Sekante in einem Punkt zusammenfallen.
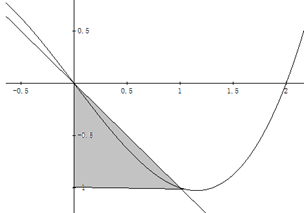
An Stelle der Tangentensteigung kann man auch zunächst eine Sekantensteigung betrachten (siehe oben). Diese ist mit etwa – 1 deutlich kleiner als die Tangentensteigung, die in Abbildung zuvor geschätzt werden konnte. Aber je kleiner wir die waagerechte Kathete der Sekantensteigung wählen, desto näher kommt die Sekantensteigung der Tangentensteigung. In der Abbildung unten ist die waagerechte Kathete h der Sekantensteigung kleiner als in der Abbildung zuvor und die Steigung der Sekante kommt der zuerst geschätzten Tangentensteigung näher.
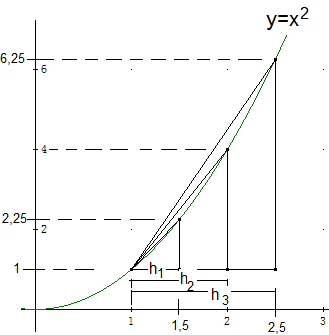
Man sagt: „Die Tangentensteigung ist der Grenzwert der Sekantensteigungen für h gegen Null.“ Mit Hilfe der Skizze unten soll die Tangentensteigung der Parabel mit der Gleichung y=x² im Punkt (1|1) angenähert werden.
Das größte der drei Steigungsdreiecke im Bild unten hat den Differenzenquotienten:
\( \dfrac{f(1+h_3)-f(1)}{h_3} \) =\( \dfrac{6,25-1}{2,5-1} = \dfrac{7}{2} \).
Das mittlere der drei Steigungsdreiecke im Bild unten hat den Differenzenquotienten:
\( \dfrac{f(1+h_2)-f(1)}{h_2} \) =\( \dfrac{4-1}{2-1} = 3 \).
Und das kleinste der drei Steigungsdreiecke im Bild unten hat den Differenzenquotienten:
\( \dfrac{f(1+h_1)-f(1)}{h_1} \) =\( \dfrac{2,25-1}{1,5-1} = \dfrac{5}{2} \).
Einfacher ist es (nicht nur hier), keine konkreten Zahlen einzusetzen, sondern den Differenzenquotienten allgemein zu berechnen:
\( \dfrac{f(x+h)-f(x)}{h} \) =\( \dfrac{(x+h)^2-x^2}{h} \) =\( \dfrac{x^2+2xh+h^2-x^2}{h} \) =\( \dfrac{2xh+h^2}{h} \) =\( \dfrac{h(2x+h)}{h} =2x+h \).
Für h=0 ist dann der Differenzenquotient allgemein gleich 2x und für x=1 ergibt sich die Steigung 2 im Punkt (1|1) der Parabel mit der Gleichung f(x)=x².
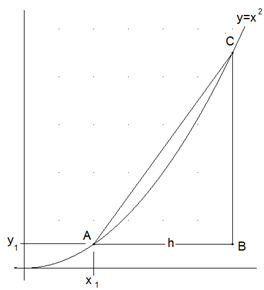
Für eine beliebige Funktion f lautet der Differenzenquotient an der Stelle x: \( \dfrac{f(x+h)-f(x)}{h} \) .
Zu einer Funktion f heißt der Grenzwert des Differenzenquotienten an einer Stelle x1 für h gegen 0 auch „Steigung“ des Graphen von f an der Stelle x1. Formal f '(x1 )=\( \lim\limits_{h\to0} \) \( \dfrac{f(x_1+h)-f(x_1)}{h} \) .
Die Begriffe
- Steigung des Graphen einer Funktion an einer Stelle x1
- Grenzwert des Differenzenquotienten von f an einer Stelle x1
- erste Ableitung von f an einer Stelle x1 (Schreibweise f ‘(x1))
sind Synonyme.
Zur Bestimmung des Grenzwertes des Differenzenquotienten von f an einer Stelle x1 ist eine Umformung des Differenzenquotienten zweckmäßig, in welcher der Nenner h herausgekürzt werden kann. Eine solche Umformung gelingt oft, insbesondere für Polynomfunktionen (aber nicht immer).