Vom Duplikat:
Titel: Flächeninhalt von Kreissektoren
Stichworte: kreis,kreissektor
Aufgabe:
Hallo und zwar uebe ich fuer eine aufkommende Pruefung und sah nun diese Aufgabe im Internet, jedoch ohne dazugehörige Lösung. Nun wuerde ich gerne wissen, wie man an die Sache hier angeht.
Vielen Dank im Voraus
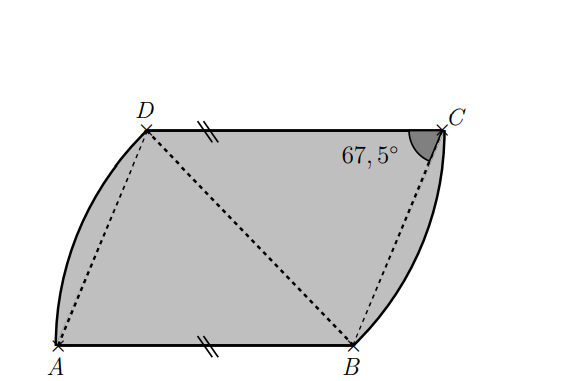
…Gegeben ist die graue Figur, die sich aus zwei
Kreissektoren zusammensetzt. Die Punkte B
und D sind die Kreismittelpunkte der Kreissektoren BDA bzw. DBC .
Die Gerade AB ist parallel zur Geraden CD.
Die Größe des Winkels ∢DCB beträgt 67, 5
◦
.
a) Begründen Sie, dass bei beiden Kreissektoren die Größe des Mittelpunktswinkels 45◦
beträgt.
b) Berechnen Sie den Umfang und den Flächeninhalt der grauen Figur, wenn CD = 10 cm.
Runden Sie Ihre Ergebnisse auf eine Dezimale.
Problem/Ansatz:
Formel fuer Kreisbogen = (α/360°)* 2π r