hier ist ein Baumdiagramm hilfreich:
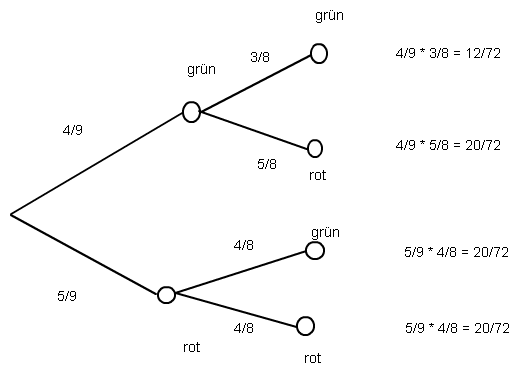
Jetzt kann man unmittelbar ablesen:
A. Grün wird im ersten Zug gezogen
Wahrscheinlichkeit dafür: 4/9
B. Grün wird im ersten und zweiten Zug gezogen
Wahrscheinlichkeit dafür: 12/72 = 6/36 = 1/6
C: Grün im zweiten Zug unter der Bedingung, dass grün bereits im ersten Zug gezogen
wurde
Wahrscheinlichkeit dafür: 3/8
Besten Gruß