Das Wort "Rundungsfehler" ist genau das richtige Stichwort!
Da kein Rechner der Welt unendlich genau mit dezimalen Nachkommazahlen rechnet
und es ohne "Bruchschreibweise" keine exakte Lösung gibt,
kann man zunächst die Genauigkeit vorgeben: 99% der Programme rechnen mit double,
was etwa 15 Nachkommastellen entspricht.
Wenn man Iterativ den Mittelwert aus den beiden gerundeten Werten bildet
und dann iterativ zurückrechnet und den neuen Wert immer wieder in diese Iteration neu einrechnet,
stellt sich nach etwa 46 Iterationen ein Gleichgewicht ein, wo es trotz Rundung und trotz
"keine perfekte Bruchrechnung" bei Rückrechnung wieder der selbe Wert für x herauskommt.
Per Iterationsrechner mit Startvorgabe aB[0]=5.03 (was Deinem x entspricht):
http://www.gerdlamprecht.de/Roemisch_JAVA.htm##@N@B0]=5.03;@C0]=(@B0]-5)/9;aD[0]=@B0]/12;a=1e5;@N@Bi+1]=(floor(aD[i]*12*a)/a+floor((@Ci]*9+5)*a)/a+@Bi]*3)/5;@Ci+1]=(@Bi+1]-5)/9;aD[i+1]=@Bi+1]/12;@Ni%3E58@N0@N1@Nb=aD[i-1]*12;c=@Ci-1]*9+5;
ergibt das online
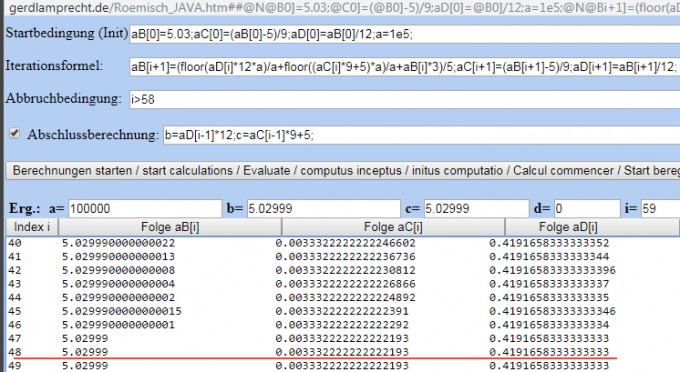
Eingeschwungenes aB[48]=5.02999 ist also Dein gesuchtes x
Die abschließende Rückrechnung zu x mit beiden Rückrechnungs-Wegen:
a) aus aD[48] (was Dein b entspricht) in Variable b
b) aus aC[48] (was Dein a entspricht) in Variable c
ergibt dann den selben Ausgangswert (für Dein x) ohne Rundungsfehler!
2 weitere Beispiele für die 3 eingeschwungen Variablen:
5.0397 0.004411111111111094 0.419975
5.04969 0.005521111111111112 0.4208075